柊四千的倉庫

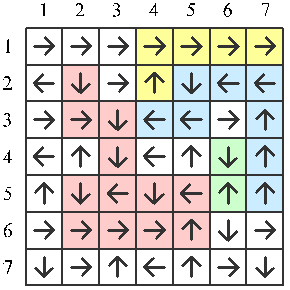
Description hellogameboy 正在進行一個神秘的計畫 他打算以 H 的力量來征服全世界，讓世界都屈服在他的 H 勢力之下 這時候正義的 hallogameboy 挺身而出，決心鼎力維持這個世界的正直 想像這世界是一個 $n\times n$ 的格子棋盤，每個格子都是一個城市 而時事潮流總有固定的流向，因此對於每個格子都有一個"潮流傳播方向" (上、下、左、右之一) 若某個城市的潮流是流向棋盤邊界外，當然，這個城市的潮流就不會傳播給任何人 hellogameboy 和 hallogameboy 將輪流展開行動， 由 hellogameboy 先展開 H 的攻勢，再換 hallogameboy 進行正直防守...... 攻防不斷交替地進行，直到所有城市都被佔領 一開始所有城市都是純潔的，沒有受到任何佔領 而 he(a)llohameboy 將選擇一個"源流城市"佔領 H (正直) 的力量就會從這個源流城市開始沿著每個格子的潮流傳播方向傳播 路上的城市都被佔領，直到某個潮流傳出邊界，或是遇到某個已被佔領的城市才停止。 以上圖為例（佔領攻防還沒結束，也不是最佳佔領策略） hellogameboy 先選擇 $(2,2)$，並佔領紅色的 $12$ 格 再來換 hallogameboy，選擇 $(5,7)$，佔領藍色的 $8$ 格 再來又輪到 hellogameboy，選擇 $(5,6)$，佔領綠色 $2$ 格 hallogameboy 再選擇 $(2,4)$，佔領黃色等 $5$ 格…… 給定一個地圖，假設 hallogameboy 和 hellogameboy 都是絕頂聰明的人物 那麼請問，最後 hellogameboy 將以 H 勢力會統領多少土地呢? Input Format 第一行為一個整數 $n$，代表地圖邊長。 再來為 $n$ 行，每行是一個不含空白的字串，由 l、r、u、d 構成，依序代表左、右、上、下的箭頭。 $1\leq n\leq 2000$ Output Format 一個整數，代表先者 (hellogameboy) 可以佔領多少格。 Sample Input 6 drludl rudlru dldldl r...

前言 要計算兩個大數的乘積，可以先把這兩個大數轉成兩個多項式，計算它們的乘積，再轉回大數，時間複雜度 $O(n\log n)$；然而，大數除法和多項式除法可說是完全不一樣的問題。以下要介紹如何利用 牛頓法 把除法問題轉化成乘法問題，並利用倍增 (doubling) 來得到 $O(n\log n)$ 的除法演算法。 本文內容大致上只是把之前我寫的 這篇 document 換成中文，但一些證明以及虛擬碼 (pseudocode) 則省略。另，實作部分可以參考我在 github 上的 大數模板 ，讀者也可以在 ZJ b960 測試自己的程式。 動機 以下設 $\xi$ 和 $\eta$ 都是 $A$ 進位正整數，其中 $A \geq 9$，$\xi \geq \eta$，且 $\xi$ 和 $\eta$ 的長度分別為 $m$ 和 $n$，目標求出 $\lfloor\xi/\eta\rfloor$ 的 $A$ 進位表示。因為 \[\xi/\eta = \xi\times 1/\eta\] 如果我們能把 $1/\eta$ 算得夠精確，就能把除法問題轉換成乘法問題。我們希望能找到某個 $x \leq 1/\eta$ 使得 \begin{equation}\label{goal}\lfloor\xi/\eta\rfloor-1 \leq \lfloor\xi x\rfloor \leq \lfloor\xi/\eta\rfloor\end{equation} 不難發現只要 $x$ 滿足 \begin{equation}\label{tol1}0 \leq 1/\eta-x \leq A^{-m}\end{equation} 就有 \[\xi/\eta-\xi x = \xi(1/\eta-x) \leq A^m\cdot A^{-m} = 1\] 也就是 $(\ref{goal})$ 會成立。接下來我們把目標放在找到 $x$ 滿足 $(\ref{tol1})$。 牛頓法 考慮函數 $f(x) := \frac{1}{x} - \eta$。我們找一個 $x_0 \in (0, \frac{1}{\eta}]$，並對於所有的 $k \geq 0$，令 \[x_{k+1}\gets x_k - \frac{f(x_k)}{f'(x_k)} = x_k(2...

整數的加減乘除四種運算，無論是在國小算術或是在程式設計中，除法都比其他三種運算來得麻煩。舉例來說，假定我們想動手算 $1650794238\div 26451$，長除法的第一步是 我們必須猜出 $\Box$ 內要填的數字，而這正是除法計算痛苦的來源。因為我們沒有表可以查，只能猜一個數字 $\alpha$，放入 $\Box$ 中，看看 $165079 - 26451\alpha$ 是否介於 $0$ 到 $26450$ 之間，而如果不幸猜錯，還得重猜並重新計算一次乘法和減法。 我們把這個猜商問題寫得再清楚一點：給定兩個 $b$ 進位的整數 \[\begin{cases}\xi = x_{n-1}\ldots x_1x_0= x_{n-1} b^{n-1} + \ldots + x_1b + x_0,\\\eta = y_{n-1}\ldots y_1y_0= y_{n-1} b^{n-1} + \ldots + y_1 b + y_0,\end{cases}\] 其中 $0 \leq x_i \leq b-1$ 對於所有的 $0 \leq i \leq n-2$，而 $x_{n-1} \geq 0$ (可以超過 $b-1$，如上面的例子 $b=10, n=5$ 而 $a_4 = 16$)。 $0 \leq y_i \leq b-1$ 對於所有的 $0 \leq i \leq n-1$，且 $y_{n-1} \neq 0$。 $\lfloor\xi/\eta\rfloor \leq b-1$。 目標找出 $a := \lfloor\xi/\eta\rfloor$。有鑑於網路上多數的大數長除法 code，猜商步驟亂寫 (無誤)，我決定在這篇導正視聽 (?)，介紹一個保證在 $O(1)$ 次內猜到 $a$ 的策略。 策略一：枚舉 $a = 0, 1, \ldots, b-1$ 最糟情況猜商次數 $\Theta(b)$，不解釋。 策略二：在 $0, 1, \ldots, b-1$ 之間做二分搜找出 $a$ 這是策略一的簡單改良，猜商次數 $\Theta(\log b)$，一樣不解釋。 策略三：利用 $x_{n-1}$ 和 $y_{n-1}$，縮小策略二的二分搜範圍 想法是這樣的：因為 \[\begin{cases}x_{n-1}b...

Description 「我與小明不相見已有二年餘了，我最不能忘記的是他的雙腿。（雖然他根本沒有）」 光陰荏苒，你如今是一位御用新聞記者，專門替國王烏龜的電視台採訪各式各樣的新聞。還記得 TIOJ 1623--國王烏龜的接駁車 嗎？大意就是國王烏龜開放死老百姓烏龜們去覲見國王，舉國上下無不歡聲雷動，一時之間各個直達皇宮接駁車的站牌前都排滿了烏龜，好不盛大！你自然被派遣過去負責採訪這場盛宴。並且他們看在你的才能，決定要讓你Live連線報導，你知道如果把這個難得的機會搞砸了你可能會變成小明第二。 因此，在開始報導之前你決定先去向前輩烏龜瞭解你的報導方式。 「 你待會要進行的報導方式呢，你看那邊有一條大排長龍的隊伍，共有 $n$ 隻烏龜排成一列，你需要選擇一個區間 $[A, B]$（包含$A, B$）進行採訪，採訪的方式是依序遞麥克風給這個區間每一隻烏龜，讓他們自由發言。必須注意的是因為要弄得看起來很有公信力，你採訪的 總人數不能小於 $L$ 個人 。 當然自由發言是有危險成份在的，有些反國王份子可能會講出危言聳聽的話，危害國王聲譽，所以我們會依序把烏龜標號 $0$ 或 $1$，$0$ 表示危險份子、$1$ 則是很安全。 所以，我們希望你能讓這個區間內 $\mathbf{1}$ 佔的比例越大越好 ，如果有很多個一樣好的區間，那就是總人數越少越好（但還是得 $\geq L$），如果還是有很多個，那就 $A$ 越小越好。 你選好你要採訪的區間了嗎？告訴我吧。 」 Input Format 輸入第一行含一個正整數 $T$，表示接下來有幾條隊伍要採訪（幾組詢問） 每組詢問第一行含兩個正整數 $n, L$（$L \leq n$），分別表示隊伍長度跟採訪總人數下限。 第二行會是一個長度為 $n$ 的 $01$ 序列，依序表現出每隻烏龜危不危險。 $T \leq 400$ $1 \leq n \leq 100,000$ Output Format 對每組詢問輸出兩個正整數數字 $A$ 和 $B$，表示 $[A,B]$ 是你的最佳選擇。 ※這個序列編號由 $1$ 開始，到 $n$ 為止。 Sample Input 2 17 5 00101011011011010 20 4 1...

Description 現在有 $n$ 輛往右邊跑的賽車，每一輛都有其固定的車速以及起始位置。 你是一位專業的攝影師，而你相信你的專業，順從你的渴望，你希望能夠抓準時機，一次把所有賽車通通照下來。 如果要把所有賽車通通照下來，那麼你的底片要夠長才行。 為了節省成本，你想要知道在所有時刻中，什麼時候最領先的車子跟最落後的車子的距離會最短。 手癢的你趕快來寫個程式求出 最短距離 吧！ Input Format 輸入的第一列有一個正整數 $n$ ($2\leq n\leq 100,000$)。 接下來有 $n$ 列，每列有兩個整數 $v_i, s_i$ 依序代表第 $i$ 輛賽車的車速(單位：公尺/秒)以及起始座標(向右為正，單位：公尺)。 ($0\leq v_i, s_i\leq 1,000,000$) 噢對了，所有車子都位於不同的賽道，因此你不必考慮它們追撞的情形，也不用考慮車身的長度。 而且你可以假設所有車子的車速都不相同。 Output Format 請輸出所有時刻中(時間 $\geq 0$)，最前面的車子與最後面的車子之最小水平間距。 只要四捨五入輸出至小數以下第二位即可。 Sample Input 3 1 1 2 0 3 0 Sample Output 0.50 Solution 這題的 $n$ 實在太大，沒辦法枚舉所有的超車事件來求出答案。注意到答案只要求到小數下第 $2$ 位，可以考慮用近似解。設 $x_i(t)$ 為第 $i$ 台車在 $t$ 秒時的位置，則題目問的就是 \[f(t) := \max_{1 \leq i \leq n} x_i(t) - \min_{1 \leq i \leq n} x_i(t)\] 在 $t \geq 0$ 的最小值。觀察到 $x_i(t) = v_i(t) + s_i$ 既是 convex function  也是 concave function ，所以 $f_1(t) := \max_{1\leq i\leq n}x_i(t)$ 是 convex function。 $f_2(t) := \min_{1\leq i\leq n}x_i(t)$ 是 concave function。 $f(t) = ...

Description 在一片山的上空，高度為 $t$ 處有 $n$ 個處於不同水平位置的燈泡，如上圖所示。 如果山的邊界上某一點與第 $i$ 盞燈的連線不經過任何山稜線上的一點，我們稱第 $i$ 盞燈可以照亮該點。 請問至少要打開幾盞燈，才能照亮山上每一個轉折點？ Input Format 輸入可能包含多筆測試資料。 對於每筆測試資料： 第 $1$ 列：一個整數 $m$ ($1\leq m\leq 100,000$)，代表山稜折線的轉折點個數。 第 $2$ ～ $m+1$ 列：$x_i, h_i$，依序代表轉折點的水平座標以及垂直海拔高度。($-100,000\leq x_i, h_i\leq 100,000$) 所有轉折點座標將以 $x$ 座標由小到大排列。 第 $m+2$ 列：$n, t$，其中 $n$ 代表燈泡個數，$t$ 代表所有燈泡的高度，該高度必定高於整座山最高轉折點的高度。 ($1\leq n, t\leq 100,000$) 第 $m+3$ 列：有 $n$ 個整數 $b_1, b_2, \ldots,  b_n$，代表 $n$ 個燈泡的水平座標，且依座標值由小到大排列。 Output Format 如果可以點亮某幾盞燈而照亮所有轉折點，請輸出最少需要點亮的燈泡數量。 否則請輸出 "you need more bulbs!"(不包含雙引號)。 Sample Input 6 1 1 3 3 4 1 7 1 8 3 11 1 4 5 1 5 6 10 6 1 1 3 3 4 1 7 1 8 3 11 1 2 5 1 5 Sample Output 2 you need more bulbs! Solution 首先，不難發現某個轉折點能被照到若且唯若有顆燈泡的位置在水平線 $y=t$ 上的某個開區間內。如果我們能求出每個轉折點對應的開區間，問題就被轉成下面這個形式：給定 $\mathbb{R}$ 上的 $m$ 個開區間 $\{(l_i, r_i)\}_{i=1}^m$，從 $b_1, \ldots, b_n \in \mathbb{R}$ 中選出...

多項式乘法常常在一些計數問題上出現，例如 UVa 12298 或  ICPC 5705 。多項式除法雖然比乘法冷門，也是有一些應用的。 問題一：給定 $n-1$ 次複係數多項式 $f(z)$ 和 $n$ 個點 $z_1, \ldots, z_n \in \mathbb{C}$，在 $O(n(\log n)^2)$ 時間內求出 $f(z_1), \ldots, f(z_n)$。 這題出自 CLRS 上的習題。設 $1 \leq l \leq r \leq n$ 並考慮 \[p(z; l, r) := \prod_{k=l}^r(z-z_k) = (z-z_l)\ldots(z-z_r)\] 觀察到 $f(z)$ 在 $z = z_l, \ldots, z_r$ 上的值，和 $f(z)\operatorname{mod}p(z; l, r)$ 在 $z = z_l, \ldots, z_r$ 上的值相同。假定 $p(z; 1, \lfloor n/2\rfloor)$ 和 $p(z; \lfloor n/2\rfloor+1, n)$ 為已知，我們可以分別計算 $f(z)\operatorname{mod}p(z;1, \lfloor n/2\rfloor)$ 在 $z = z_1, \ldots, z_{\lfloor n/2\rfloor}$ 的值 $f(z)\operatorname{mod}p(z; \lfloor n/2\rfloor+1, n)$ 在 $z = z_{\lfloor n/2\rfloor+1}, \ldots, z_n$ 的值 這樣的 divide and conquer 時間複雜度是 $T(n) = 2T(n/2) + O(n\log n) = O(n(\log n)^2)$。 那麼要怎麼求出過程中需要的 $p(z; l, r)$ 們呢？回想一下，計算 $p(z; 1, n) = p(z;1, \lfloor n/2\rfloor)p(z; \lfloor n/2\rfloor+1, n)$ 有一個顯然的 D&C 做法，時間複雜度也是 $O(n(\log n)^2)$，且中間過程算到的 $p(z; l, r)$ 們正好就是前一個 D&C 所需要的 $p(z; l, r)$ 們。這樣...

計算兩個不超過 $n$ 次的複係數一元多項式 $f(x)$ 和 $g(x)$ 的乘積，可以藉由 FFT (Fast Fourier Transform, 快速傅立葉變換) 在 $O(n\log n)$ 時間內求得。更一般的情形，設 $R$ 為一個環且 $f(x), g(x) \in R[x]$，則 $f(x)g(x)$ 可以用 Karatsuba 演算法 在 $O(n^{\log_23})$ 時間內求得，也比 naïve 演算法的 $O(n^2)$ 快。假設多項式乘法的時間複雜度是 $O(M(n))$，這篇將介紹如何在 $O(M(n))$ 時間內計算 $f(x)\div g(x)$ 的商式和餘式。 先定義好我們的問題：設 $R$ 為一個有 $1$ 的環，$f(x), g(x) \in R[x]$ 滿足 $\deg f = n$ $g(x) \neq 0, \deg g = m \leq n$ $g$ 的 $x^m$ 項係數為 $1$ 我們要找出 $q(x), r(x) \in R[x]$ 使得 $f(x) = q(x)g(x) + r(x)$ $\deg r < m$ 不難從長除法證明 $q$ 和 $r$ 存在且唯一。接著，引入反轉算子 $\mathscr{R}: R[x] \to R[x]$，定義對於所有的 $h(x) \in R[x]$， \[(\mathscr{R}h)(x) = \begin{cases}0,&\text{if }h(x) = 0,\\x^ph(\frac{1}{x}),&\text{if }\deg h = p.\end{cases}\] 事實上，若 $h(x) = \alpha_0 + \sum_{i=1}^p\alpha_ix^i \neq 0$，則 $(\mathscr{R}h)(x) = \alpha_p+\sum_{i=1}^p\alpha_{p-i}x^i$。這樣一來，就有 \[(\mathscr{R}f)(x) = \begin{cases}(\mathscr{R}q)(x)\cdot(\mathscr{R}g)(x),&\text{if }r(x) = 0,\\(\mathscr{R}q)(x)\cdot(\mathscr{R}g)(x)+x^{n-\d...

Description 楓之谷是個平面捲動的線上遊戲，在這遊戲裡面，除了讓玩家不停地打怪物賺經驗值升級以外，還安排了一些「任務」給玩家解，只要完成了，就會有特別的獎勵。有的任務是收集一定數量的特定物品，而有的任務叫作「忍耐任務」。 顧名思義，忍耐任務就是在考驗玩家的耐性。在忍耐任務裡面，玩家會被差派到特別的地圖去，在這種地圖裡面，也許還是會有怪物，並且會有一些飛來飛去的飛行物，像是飛鏢一類的，然而當它們撞到玩家的時候，玩家幾乎不會損血，因為它們存在的意義並不是要將玩家擊斃，而只是要阻礙玩家前進。在這樣的地圖裡，通常會安排十分難走的路，例如說有非常小的平台來讓玩家跳躍，或是不時會有長矛刺到的繩梯，而且在路途上還安排了會阻礙玩家的飛行物和怪物，玩家只要一個不小心，就會掉下來。這路途常安排得十分漫長，而且一掉下來，就要重頭來過。而玩家的最終目標，就是要走完全程，拿到指定的物品，或是和指定的人物說話。 很難想像什麼人會喜歡解這種任務，可是真的有人熱中於此，甚至成為此間箇中高中。暱稱是阿特珞的這位玩家，就是這樣的一個奇人，她不但解自己接的忍耐任務，還幫忙別人解，甚至挑戰十五分鐘內解三個，熟練的程度甚至在遊戲中曾讓別人懷疑她是否使用外掛輔助程式。 成功的行動寓於周詳的計畫，在解一個任務之前，她已將這個地圖的底細調查清楚了。知道哪些地方有平台可以站立，也知道所有的飛行物體的軌跡和週期。然後她擬定了一連串的移動計畫，也就是在什麼時候要做什麼動作，像是蹲下，移動，或是跳躍。提供了周詳的地圖與計劃內容後，她想請你們寫一個程式，判斷她所擬定的計劃是否能成功執行。 Input Format 在這輸入的資料裡，總共包含一個場景，還有若干個移動計畫。我們假設這個場景是放在一個無窮大的二維的 $x-y$ 坐標系上。輸入的第一行將有一個整數 $l$ ($1 \leq l \leq 20$)，代表之後將會輸入 $l$ 個水平線段，它們彼此不會相交或接觸。這些線段就是在地圖中可以站立的地方，(另外在跳躍的時候並不會因為頂到線段而掉下來。甚至當你正在往上「飛」的時候，你可以穿越上方的線段，直到下落的時候，才會停在線段上。) 每一行會包含一條線段的輸入資料，共有三個數 (可能有小數點)，第一個數是這個線段的 $y$ 坐標，第二個數是左側 (較小) 端點的 $x$ 坐標，第三個數是右側...