由14個點組成的5-正則圖必不是平面圖

我們用反證法證明結論。假定存在 $5$-正則平面圖 $G_0$ 且 $|V(G_0)|=14$，不妨設 $G_0$ 已經嵌入(embed) $\mathbb{R}^2$ 裡了。首先觀察到 $$|E(G_0)| = \frac{1}{2} \cdot 5 \cdot 14 = 35.$$ 另一方面，平面圖的邊數上限給出 $3|V(G_0)| - 6 = 36$，我們可以得到以下的引理：

[引理 1] $G_0$ 恰包含一個 $4$ 邊組成的面 (face)。

我們加一條邊在 $G_0$ 唯一的 $4$ 邊組成的面，得到新的平面圖 $G$。$G$ 會滿足以下的性質：

1. $G$ 有 $12$ 個點的度數為 $5$ 且有 $2$ 個點的度數為 $6$。
2. $G$ 上度數為 $6$ 的兩個點相鄰。
3. $G$ 的每個面都是三角形，且每條邊恰好夾在兩個面中間。

一個平面圖上的簡單環 $C$ 會將這個平面圖的點集合切成三塊：$C$ 內部的點 $V_\text{in}(C)$、$C$ 外部的點 $V_\text{out}(C)$、以及 $C$ 上的點 $V(C)$。我們有以下的兩個引理：

[引理 2] $G$ 的每個三角形都是面。

假定引理為假，即 $G$ 有個三角形 $x_1x_2x_3$ 滿足 $|V_\text{in}(x_1x_2x_3)|$ 與 $|V_\text{out}(x_1x_2x_3)|$ 皆不為 $0$。 由於 $|V_\text{in}(x_1x_2x_3)| + |V_\text{out}(x_1x_2x_3)| = 11$，我們可以假設 $|V_\text{in}(x_1x_2x_3)| \le 5$。 另一方面，由於 $G$ 裡所有點的度數皆至少為 $5$，必須有 $|V_\text{in}(x_1x_2x_3)| \ge 3$。

情況 1：$|V_\text{in}(x_1x_2x_3)| = 3$

由於對任意 $v \in V(G)$ 皆有 $\deg(v) \ge 5$，我們發現導出子圖 (induced subgraph) $G[V_\text{in}(x_1x_2x_3)\cup\{x_1, x_2, x_3\}] \cong K_6$，包含了 $K_5$ 結構，與 $G$ 為平面圖矛盾。

情況 2：$|V_\text{in}(x_1x_2x_3)| = 4$

設 $x_1x_2, x_2x_3, x_3x_1$ 向內的面分別為 $x_1x_2v_1, x_2x_3v_2, x_3x_1v_3$。 首先我們有 $v_1, v_2, v_3$ 兩兩相異（否則 $x_1x_2x_3$ 就分成 $3$ 個三角形，但其中一個包含 $3$ 個以下的頂點）， 設 $V_\text{in}(x_1x_2x_3) = \{v_1, v_2, v_3, v_4\}$ 以及 $H := G[V_\text{in}(x_1x_2x_3)\cup\{x_1, x_2, x_3\}]$。 握手引理 (handshaking lemma) 告訴我們 $$2|E(H)| \ge \underbrace{3 \cdot 4}_{x_i\text{'s}} + \underbrace{4 \cdot 5}_{v_i\text{'s}} = 32 \quad \Rightarrow \quad |E(H)| \ge 16.$$ 另一方面，由於 $H$ 是平面圖，我們有 $$|E(H)| \le 3|V(H)|-6 = 15.\quad(\to\gets)$$

情況 3：$|V_\text{in}(x_1x_2x_3)| = 5$

設 $V_\text{in}(x_1x_2x_3) = \{v_1, v_2, v_3, v_4, v_5\}$，其中 $x_ix_{i+1}$ 向內的面為 $x_ix_{i+1}v_i$（這裡定義 $x_4 = x_1$）。 握手引理告訴我們 $$2|E(H)| \ge \underbrace{3 \cdot 4}_{x_i\text{'s}} + \underbrace{5 \cdot 5}_{v_i\text{'s}} = 37 \quad \Rightarrow \quad |E(H)| \ge 19.$$ 另一方面，由於 $H$ 是平面圖，我們有 $$|E(H)| \le 3|V(H)|-6 = 18.\quad(\to\gets)\tag*{$\blacksquare$}$$

[引理 3] $G$ 的每個長度為 $4$ 的簡單環 $Q$ 滿足 $|V_\text{in}(Q)| = 0$ 或 $|V_\text{out}(Q)| = 0$。

假設引理為假，即存在某個長度為 $4$ 的簡單環 $Q$ 使得 $|V_\text{in}(Q)| > 0$ 且 $|V_\text{out}(Q)| > 0$。 由於 $|V_\text{in}(Q)| + |V_\text{out}(Q)| = 10$，我們可以假設 $|V_\text{in}(Q)| \le 5$。 另一方面，由於 $G$ 裡所有點的度數皆至少為 $5$，必須有 $|V_\text{in}(Q)| \ge 2$。 本節令 $H$ 為導出子圖 $G[V(Q) \cup V_\text{in}(Q)]$。

情況 1：$|V_\text{in}(Q)| = 2$

$H$ 必定有個子圖如下，包含了 $K_{3, 3}$，與 $G$ 為平面圖矛盾。

情況 2：$|V_\text{in}(Q)| = 3$

觀察 $$\begin{split} |E(H)| &= \underbrace{|E(G[V(Q)])|}_\text{outer part} + \underbrace{\sum_{v \in V_\text{in}(Q)} \deg_G(v)}_\text{#\{edges connecting inner and outer parts\} + 2(inner part)} - \underbrace{|E(G[V_\text{in}(Q)])|}_\text{inner part}\\ &\ge 4 + 3 \cdot 5 - 3 = 16. \end{split}$$ 另一方面，由於 $H$ 是平面圖，必須滿足 $$|E(H)| \le 3|V(H)|-6 = 15.\quad(\to\gets)$$

情況 3：$|V_\text{in}(Q)| = 4$

令 $Q = x_1x_2x_3x_4$ 並設 $x_ix_{i+1}$ 向內的面為 $x_ix_{i+1}v_i$（這裡定義 $x_5 = x_1$）。 我們說明 $v_1, v_2, v_3, v_4$ 必定兩兩相異。 若 $v_1 = v_2$ 或 $v_1 = v_3$，則 $Q$ 被切成三角形 $x_1x_2v_1, x_2x_3v_1$ 以及長度為 $4$ 的環 $x_3x_4x_1v_1$。 這 $3$ 塊區域必定有一塊內部包含不超過 $3$ 個點，矛盾。

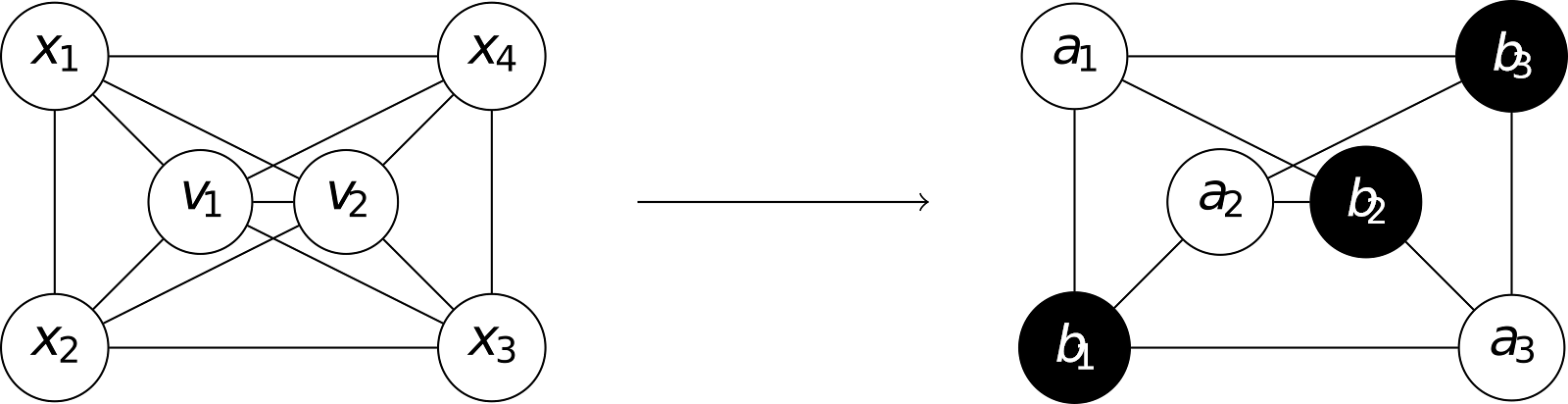
此時 $H$ 必定有個子圖如下，包含了 $K_{3, 3}$ 的細分圖 (subdivision)，與 $G$ 為平面圖矛盾。

情況 4：$|V_\text{in}(Q)| = 5$

採用與情況 3 相同的變數假設，並令 $V_\text{in}(Q)$ 的第 $5$ 個點為 $v_5$。 由於 $\deg_H(v_5) = \deg_G(v_5) \ge 5$，$v_5$ 必定與某個 $x_i$ 相鄰，不妨設之為 $x_1$。 此時 $v_5$ 不能與 $x_2, x_3, x_4$ 相鄰（否則 $Q$ 又被切成更小的三角形或長度為 $4$ 的環），故 $H$ 必定有個子圖如下：

此子圖包含了 $K_{3, 3}$ 的細分圖，與 $G$ 為平面圖矛盾。$\tag*{$\blacksquare$}$

有了上述的兩個引理我們準備完成證明了。 設 $v \in V(G)$ 且 $\deg(v) = 6$，並設 $v$ 的鄰居們為 $U := \{u_1, u_2, \ldots, u_6\}$，其中 $u_i$ 與 $u_{i+1}$ 相鄰（這裡 $u_7 := u_1$）。 由引理 2 得知 $u_1$ 不能與 $u_3$ 或 $u_4$ 相鄰，故 $G[U] \cong C_6$。

設 $u_iu_{i+1}$ 在另一個面 $u_iu_{i+1}w_i$ 上。 我們有 $w_1, w_2, \ldots, w_6$ 兩兩相異，因為若 $w_1 = w_i$，其中 $i = 2, 3, 4$，則可以找到一個長度為 $4$ 的環 $Q_i := u_1vu_{i+1}w_1$，但 $|V_\text{in}(Q_i)|$ 與 $|V_\text{out}(Q_i)|$ 皆不為 $0$，與引理 3 矛盾。

最後，回想一下 $G$ 的兩個度數為 $6$ 的點是相鄰的，不妨設 $\deg(u_1) = 6$，以及 $u_1$ 的第 $6$ 個鄰居是 $w$。 若 $w = w_2$ 或 $w = w_3$，則可以找到 $Q := u_1wu_3v$，但 $|V_\text{in}(Q)|$ 與 $|V_\text{out}(Q)|$ 皆不為 $0$，與引理 3 矛盾。

如此一來 $w$ 就是 $G$ 的最後一個點了。 假定 $w$ 與 $w_2$ 相鄰，則可以找到 $Q := u_1ww_2u_2$，但 $|V_\text{in}(Q)|$ 與 $|V_\text{out}(Q)|$ 皆不為 $0$，再一次地與引理 3 矛盾。

所以 $w$ 的鄰居只能是 $u_1, w_1, w_3, w_4, w_6$，但此時 $\deg(w_2)$ 最大只能是 $4$，矛盾，定理至此證畢。