水母上 Divide-and-Conquer

一棵樹有「拔掉任一非葉節點便不連通」的良好性質，可以幫助我們用 DP 和 divide-and-conquer 解決問題，例如 POJ 1741 和 TIOJ 1647。這篇假定你知道怎麼把 POJ 1741 做到 $O(n(\log n)^2)$ 的時間複雜度 (如果你不知道也沒關係，google "POJ 1741" 就有很多資料了 XD)。我們沿用先前的定義，把一張點數和邊數相等的連通近圖 (pseudograph) 稱作一隻水母。再次提醒，水母並不是正式名稱 (我找不到正式名稱 orz)。

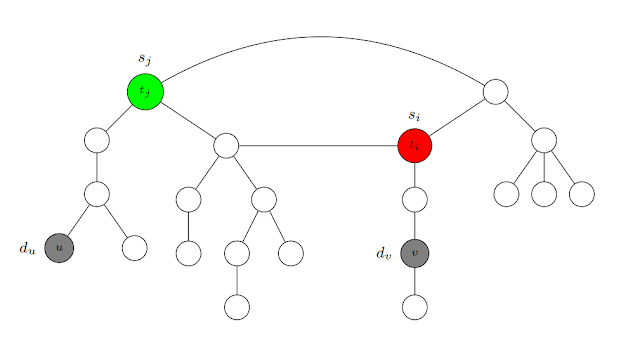
考慮這個問題：給定一隻大小為 $n$ 的水母 $J = (V, E)$，邊有正權重，請求出 $J$ 的 $K$-近對個數。一個 $K$-近對的定義是距離不超過 $K$ 的 (無序) 點對。觀察到一隻水母其實是由頭部 (環) 和數條觸手 (樹) 組成。設頭部由點 $t_0, t_1, \ldots, t_{m-1}$ 組成，從 $t_i$ 長出的觸手為 $T_i$。我們把 $K$-近對 $(u, v)$ 分成兩種：$u, v$ 屬於同一條觸手 ($\alpha$ 型)、$u, v$ 屬於不同條觸手 ($\beta$ 型)。只要在每條觸手上跑 POJ 1741，就能求出 $\alpha$ 型 $K$-近對個數了。至於 $\beta$ 型，做法是對於每個點 $v$，統計有幾個點 $u$ 滿足

1. $u$ 和 $v$ 不在同一條觸手上
2. $u, v$ 的距離 $d(u, v) \leq K$

我們用上圖來做說明。設邊 $(t_i, t_{i+1})$ 的權重為 $w_{i+1}$，$s_i := w_1 + \ldots + w_i$ 為「從 $t_0$ 開始，順著 $t_0, t_1, t_2, \ldots$ 的方向，走 $i$ 條邊的里程數」(為了方便，不該超過 $m-1$ 的那些索引值，一旦超過 $m-1$ 就自動對 $m$ 取模)。設 $$\begin{cases} u \in T_j, d_u := d(u, t_j),\\ v \in T_i, d_v := d(v, t_i), \end{cases}$$ 則 $d(u, v)$ 就是 $d_u+d_v+(s_i-s_j)$?! 當然我們沒有這麼好的事情，因為

1. 有可能 $i < j$
2. 即使 $i > j$，可能 $s_i-s_j > s_m/2$，也就是 $d(t_i, t_j) = s_m-(s_i-s_j) < s_i-s_j$

對於第一種情況，解決方法是多繞頭部一圈，用 $s_{m+i}-s_j$ 取代 $s_i-s_j$。至於第二種情況，其實可以只統計「滿足 $s_i-s_j \leq s_m/2$ 的那些 $u$」就好了：如果 $s_i-s_j > s_m/2$，則 $s_{m+j}-s_i = s_m-(s_i-s_j) < s_m/2$，因此這種 $(u, v)$ 會在「對 $u$ 統計」時被算到。

那麼要怎麼統計有幾個 $u$ 滿足 $d_u+d_v+(s_i-s_j)\leq K$ 呢？固定 $v$，我們想知道的其實是有幾個 $u$ 滿足 $d_u-s_j \leq K-d_v-s_i$。如果我們有一棵 binary search tree 儲存 $d_u-s_j$ 們，就能在 $O(\log n)$ 時間內得到答案。統計完 $v \in T_i$ 後，換統計 $v \in T_{i+1}$，此時 $T_i$ 裡的 $d_u-s_i$ 們可以加進 BST 中；另一方面，可能有些 $j$ 變成 $s_{i+1}-s_j > s_m/2$，必須把這些 $T_j$ 裡的 $d_u-s_j$ 們從 BST 踢掉。詳細部分可以參考下面這份 pseudocode：

計算 $\alpha$ 型 $K$-近對個數需要 $O(n(\log n)^2)$ 時間，而計算 $\beta$ 型 $K$-近對個數需要 $O(n\log n)$ 時間 (對 BST 插入 $2n$ 次、查詢 $n$ 次、與刪除不超過 $2n$ 次)，因此整體的時間複雜度只有 $O(n(\log n)^2)$。

這題可以在 ZJ a666 測。