110 學年度全國資訊學科能力競賽各題詳解

筆者這次也參與了全國賽的驗題，這邊放一份另一位驗題者與筆者提供的詳解。題本的連結在這裡，pC / pE / pH / pI 的時間限制分別為 2.5s / 2.5s / 2.0s / 0.1s，其餘題目皆為 1.0s。另，讀者也能在這裡找到與下文基本相同的內容。

A. 髮廊服務優化問題 (barbershop)

有 $n$ 個人一起來店，第 $i$ 個人的服務時間為 $t_i$。每個客人等待時間是前面人 $+$ 自己服務時間總和，求等待時間總和的最小值。例如：三個人服務時間為 $2,1,3$，若服務順序為 $1,2,3$ 則等待時間總和為 $2 + (2+1) + (2+1+3) = 11$。

等價題序：給一個陣列 $\mathbf{t} := \{t_i\}_{i=1}^n$，將 $\mathbf{t}$ 重新排列使得 $nt_1 + (n-1)t_2 + (n-2)t_3 + \ldots + t_n$ 最小。由上式不難得知，順序越前面被乘的係數就越大，所以可以貪心地將數字從小排到大。複雜度 $O(n \log n)$。

B. 校園公車 (bus)

給定由 $n$ 條線段組成的折線 $\mathbf{P} := \left\{ \overline{P_i P_{i+1}} \right\}_{i=1}^n$ 與一點 $O$，問 $O$ 到 $\mathbf{P}$ 的最短距離。

先考慮這個問題：給定一線段 $\overline{PQ}$ 與一點 $O$，求 $O$ 到 $\overline{PQ}$ 的距離。首先我們作 $O$ 到 $\overline{PQ}$ 的垂足 $H$，並試著計算 $\overline{OH}$。注意 $\overline{OH}$ 其實就是 $\Delta OPQ$ 以 $\overline{PQ}$ 為底時的高，所以可以用下面的方法計算：

Length_OH(O: Point, PQ: Segment):
    A ← ΔOPQ
    return 2A/|PQ|

$\Delta OPQ$ 可以用 Shoelace formula 計算。

但事情沒有這麼簡單。$O$ 到 $\overline{PQ}$ 的距離並不總是 $\overline{OH}$：當 $\angle OPQ$ 或 $\angle OQP$ 為鈍角時，$H$ 並不在 $\overline{PQ}$ 上，而此時的最短距離是 $\overline{OP}$ 或 $\overline{OQ}$。由畢氏定理可知，$\angle OPQ$ 為鈍角的充要條件是 $\overline{OP}^2 + \overline{PQ}^2 < \overline{OQ}^2$，因此 $O$ 到 $\overline{PQ}$ 間的距離就可以用下面的方法計算：

Distance(O: Point, PQ: Segment):
    if |OP|^2 + |PQ|^2 < |OQ|^2 then
        return |OP|
    else if |OQ|^2 + |PQ|^2 < |OP|^2 then
        return |OQ|
    else
        return Length_OH(O, PQ)
    end if

代入 $\overline{PQ} = \overline{P_1P_2}, \overline{P_2P_3}, \ldots, \overline{P_nP_{n+1}}$ 並取最小值就是答案。

C. 街頭藝人 (busker)

給一張 $n$ 點（城市） $m$ 邊的有向圖 $G_0$。我們對 $G_0$ 的每條邊都加上 $k$ 個點（村莊），得到一張 $n + mk$ 節點的有向圖 $G$，並賦予點權重 $c: V(G) \to \mathbb{Z}$（每個節點的收支）。設 $C$ 是 $G$ 上的一個簡單環且 $u \in V(C)$。若從 $u$ 出發沿著 $C$ 走一圈，任意前綴點權重和（所持金）都 $\ge0$，我們就說 $C$ 是 $G$ 的一個好環，而 $u$ 是 $C$ 的一個好起點。請找出 $G$ 的任一個好環 $C$ 與 $C$ 的任一個好起點 $u$，並求出 $C$ 上有幾個點可以當作好起點，這些好起點又有幾個在 $G_0$ 上。

非負環必可以找到好起點

顯然一個好環有點權重和 $\ge0$。我們證明若一個環的點權重和 $\ge0$，則它必定是一個好環（i.e. 可以找到一個好起點）。

設 $C$ 是一個點權重和 $\ge0$ 的環。隨意找一個 $u_1 \in V(C)$，並設從 $u_1$ 沿著 $C$ 出發走一圈經過的點依序是 $u_2, u_3, \ldots, u_{|V(C)|}$。對於所有的 $i \in \{0, 1, …, |V(C)|\}$，考慮在每個節點的所持金數列 $s$（也就是環的點權前綴和）：

\[s(i) = \begin{cases}0,&\text{if }i=0,\\\ c(u_1) + c(u_2) + \ldots + c(u_i),&\text{if }i\ge1.\end{cases}\]

考慮路途任一所持金最小的時刻 $k\in\{0, 1, \ldots, |V(C)|-1\}$，也就是 $k$ 滿足

\[s(k) = \min_{0 \le i \le |V(C)| - 1} s(i).\]

注意我們有 $s(|V(C)|) \ge 0 = s(0)$，因此

\[s(k) = \min_{0 \le i \le |V(C)|} s(i).\]

接著證明 $u_{k+1}$ 是一個好起點。

對於所有的 $i\in\{k+1, k+2, \ldots, |V(C)|\}$，從 $u_{k+1}$ 出發沿著 $C$ 走到 $u_i$ 的點權重和是 $s(i) - s(k)$，但 $s(k)\le s(i)$，故 $s(i)-s(k)\ge0$。

對於 $i\in\{1, 2, \ldots, k\}$，從 $u_{k+1}$ 出發沿著 $C$ 走到 $u_i$ 的點權重和是 $s(|V(C)|) + s(i) - s(k)$。但 $s(|V(C)|)\ge0$，依然有 $s(|V(C)|) + s(i) - s(k) \ge s(i) - s(k) \ge 0$。

非負環求好起點的數量

到前面為止，已經證明了任意一個非負環必定存在一個好起點（也就是題目所求的入能敷出演藝路線）。這裡假設讀者已經很熟悉 $O(VE)$ 找負環的技巧。接著來處理題目的另一個詢問，也就是環上共有幾個好起點。

方法 1：DP

定義 $s$ 的前綴最小值 $\alpha_i$ 為 $u_1$ 沿著 $C$ 走到 $u_i$ 時的最小所持金：

\[\alpha_i = \min_{0 \le k \le i} s(i).\]

類似地，我們也可以定義 $s$ 的後綴最小值 $\beta$：

\[\beta_i = \min_{i \le k \le |V(C)|} s(i).\]

若改變起點從 $u_x$ 開始沿著 $C$ 走一圈，可以推出所持金最小的時刻如下:

  • $u_x$ 至 $u_{|V(C)|}$ 間：$\beta_x-s(x-1)$
  • $u_1$ 至 $u_{x-1}$ 間：$\alpha_{x-1}+s(|V(C)|)-s(x-1)$
  • 上面兩者取最小值即可求得以 $u_x$ 為起點繞 $C$ 走一圈的最小所持金

由於環展開頂多只有 $n + mk$ 個節點，故這邊複雜度為 $O(n + mk)$。

方法 2：

不失一般性假定 $k=0$，亦即任意時間所持金皆非負，對於所有的 $i$ 皆有 $s(i)\ge0$。接著證明 $u_i$ 是好起點若且唯若 $s(i-1)\le s(j)$ for all $j\in\{i, i+1, \ldots, |V(C)|\}$。

  1. 若 $j\ge i$，從 $u_i$ 沿著 $C$ 走到 $u_j$ 的點權重和是 $s(j) - s(i-1)$，故 $\Rightarrow$ 是直接結論。
  2. 若 $j<i$，從 $u_i$ 沿著 $C$ 走到 $u_j$ 的點權重和變成 $s(|V(C)|) + s(j) - s(i-1)$，又因為 $s(j)\ge0$，我們有 \[s(|V(C)|) + s(j) - s(i-1) \ge s(|V(C)|) - s(i-1) \ge 0,\] 這給出了 $\Leftarrow$ 的證明。

因此只要找出了一個非負環，就能在 $O(|C|)=O(n+mk)$ 時間求出所有的好起點。

Subtask 1: $n\le20$

直接建立 $G$，注意我們有 $|V(G)| = n + mk = O(n^3)$ 且 $|E(G)| = m(k+1) = O(n^3)$。對於每條邊 $(u, v)$，轉移權重 $c(u)$。用 Bellman–Ford 演算法找出一個非負環，時間複雜度為 $O(|V(G)||E(G)|) = O(n^6)$。

Subtask 2: $n\le90$

在 Subtask 1 中，Bellman–Ford 的節點更新次數只要達到 $n$，就找到一個非負環了，故時間複雜度進一步降成 $O(n|E(G)|) = O(n^4)$。

Subtask 3: $n\le2000, m\le8000$

我們建圖的目的是找出好環，所以可以在 $G_0$ 上找出非負環 $C_0$，復原成 $C$ 後再找出好起點。設 $(u, v) \in E(G_0)$ 且在 $G$ 上被加入的點權重分別是 $a_1, a_2, \ldots, a_k$，則我們直接轉移權重 $c(u)+\sum a_i$ 到 $(u, v)$ 上，如此一來 Bellman–Ford 的時間就降為 $O(mn)$。

D. 汽車不再繞圈圈 (car)

給一張 $n$ 點 $m$ 邊的有向圖，每條邊都可以反轉，但反轉第 $i$ 條邊需要權限 $c_i$，反轉複數條邊所需的權限值就是反轉邊的最大權限。問至少要有多少權限才可以將邊反轉使得整張圖沒有環？並輸出反轉方案。

Subtask 1: $n,m\le20$

可以枚舉要反轉邊的 subset，之後再檢查環有沒有被刪掉。

Subtask 2: $c_i\le100$

答案 $=$ 選的邊裡的最大權重，直接枚舉這個數字 $x$，代表可以將權限 $x$ 以下的所有邊做任意反轉操作。至於要怎麼求出方案以及判斷 $x$ 是否是可行解，這裡提供一個方法：

  1. 首先將 $\le x$ 的所有邊刪除，做 $>x$ 邊的拓樸排序。
  2. 由於 $\le x$ 的邊可以任意改動方向，我們就改動邊的方向來符合上個步驟求出的拓樸順序。

在決定 $x$ 以後可以花 $O(n + m)$ 的時間檢查並求出可行解，複雜度是 $O(c(n + m))$。

Subtask 3: $n, m\le10^5, c_i\le10^9$

在 subtask 2 中我們已經知道了枚舉一個解的權限值判斷是否可行的方法。可以發現，若枚舉的解越大，可以改動的邊越多，也更有可能存在可行解，存在單調性。因此我們可以將 subtask 2 中枚舉權重的部分改成二分搜尋，在 $O((n + m)\log c)$ 的時間做完。當然也能先將邊權 $c_1, \ldots, c_m$ 排序，再對排序後的 $c_i$ 們做二分搜，時間複雜度進一步降成 $O((n+m)\log m)$。

E. 天空競技場 (colosseum)

有座 $n$ 層樓的競技場，其中第 $i$ 層開設時間、金幣枚數門檻、挑戰費時、結束後獲得金幣枚數分別為 $x_i, y_i, t_i, w_i$。參賽者初始擁有的金幣枚數為 $0$，但可以從任一層開始挑戰。在抵達第 $i$ 層時：

  • 若已擁有 $\ge y_i$ 枚金幣且抵達時間 $<x$，可以選擇等待競技開始或直接進入第 $i+1$ 層
  • 若已擁有 $\ge y_i$ 枚金幣且抵達時間 $\ge x$ 就一定要花 $t_i$ 時間參加競技
  • 否則只能直接進入第 $i+1$ 層

請問參賽者在時間 $m$ 時能獲得的最大金幣數量是多少？本題 $n\le300000$ 且 $1\le w_i\le1000$。

Subtask 2: $x_i=y_i=0$

用兩個 pointer 來模擬 queue，找出在 $t_i$ 區間和不超過 $m$ 的情況下，$w_i$ 區間和的最大值，時間複雜度是 $O(n)$。

Subtask 3: $x_i=0$

由於每一層只要達到門檻數量的金幣就會發生戰鬥，可以用一個 queue $Q$ 來儲存金幣數 $f$ 與時間 $s$，並依序考慮第 $1$ 層到第 $n$ 層。加入第 $i$ 層時，先把 $(0, 0)$ 插入 $Q$ 的後端，接著將 $f\ge y_i$ 的 $(f, s)$ 們全部加上 $(w_i, t_i)$，最後再從 $Q$ 的前端踢掉 $s>m$ 的那些 $(f, s)$ 們。可以得到一個 $O(n^2)$ 時間複雜度的做法，再用 Fenwick tree 進一步加速到 $O(n\log n)$。

Subtask 1: $n\le1000$

在金幣數相同的情況下，可以知道時間比較早的不會比較差。我們用一個 hash map $M$ 來儲存金幣數 $f$ (key type) 與時間 $s$ (mapped type)，並依序考慮第 $1$ 層到第 $n$ 層。加入第 $i$ 層時，先加入 $(0, 0)$ 至 $M$ 中，接著對於 $M$ 裡所有滿足 $f\ge y_i$ 的 $(f, s)$ 數對，做下面這件事情：

  1. 若 $s\ge x_i$，則把 $(f, s)$ 踢掉，並根據 $s + t_i$ 是否超過 $m$ 決定要不要加入 $(f + w_i, s + t_i)$ 至 $M$ 中。
  2. 否則，根據 $x_i+t_i$ 是否超過 $m$，決定要不要加入 $(f+w_i, x_i+t_i)$ 至 $M$ 中。

$|M|$ 最大為 $\sum w_i+1$，總共做 $n$ 次，時間複雜度為 $O(n\sum w_i)$。

滿分做法（並沒有）

在驗題的過程中，我們誤以為時間越早金幣越多越好，但這是不正確的。考慮 $m = 10, \mathbf{x} = \{0, 0, 3, 0, 0\}, \mathbf{y} = \{0, 0, 10, 110, 0\}, \mathbf{t} = \{1, 1, 1, 5, 5\}, \mathbf{w} = \{100, 10, 1, 1, 1000\}$。最佳解是從第 $2$ 層出發，第 $3$ 層等待，最後得到的 $1011$ 枚金幣（這時離開第 $3$ 層的時間與金幣數分別為 $4$ 與 $11$）。另一方面，若從第 $1$ 層出發且第 $3$ 層不等待，則離開第 $3$ 層的時間與金幣數分別為 $2$ 與 $110$，看似比前者為優，但因過了 $y_4=110$ 的門檻被強迫參加第 $4$ 層的競技，最後只能拿到 $111$ 枚金幣。

基本上這種測試資料需要特別構造。由於比賽時的測資是隨機生成的，在我們的機器上平行跑了時間複雜度 $O(n\sum w_i)$ 的解 $12$ 小時後終於確認比賽時的輸入輸出都是對的，只是這個執行時間根本不可能過得了時限。

F. 挑水果 (fruit)

  • 一開始船上有 $c$ 個種類的水果，第 $i$ 種類有 $n_i$ 顆
  • 依序經過 $c$ 個城市，每經過一個城市可以決定要不要把船上所有前 $i$ 種類的水果給當地盤商賣
  • 積載每顆水果經過都市 $i$ 需要積載成本 $p_i$
  • 把每顆水果給都市 $i$ 的盤商賣需要成本 $s_i$
  • 在都市 $i$ 賣種類 $j$ 的水果最後只會賣出 $r_{i, j}$ 顆

問若積載成本和銷售成本總和不超過 $T$ 的前提下，最多能賣幾顆水果？限制：

  • $1\le c, n_i\le40$
  • $1\le p_i, s_i\le1000$
  • $T\le10^7$

Subtask 1: $c\le20, T\le30000$

直接枚舉所有可能的銷售都市集合，組合數為 $\Omega(2^c)$。

Subtask 2: $T\le30000$

考慮 DP 狀態 $\text{dp}[i][j]$：

  • $i$ 是最後一次卸貨給盤商銷售的城市（$=$ 賣出最大的水果種類）
  • $j$ 是到城市 $i$ 卸貨為止前 $i$ 種類水果積載 $+$ 銷售的費用和
  • $\text{dp}[i][j]$ 為最後一次在城市 $i$ 卸貨，前 $i$ 種水果總花費 $j$ 時最大賣出的水果數量
  • 特殊地，若 $i=0$ 則代表尚未卸貨

枚舉 $i$ 的上一個卸貨點 $k$（$0\le k<i$）：

  • 最後一次卸貨所卸的水果種類為 $k+1$ 至 $i$，令 $N =$ 船上 $k+1$ 至 $i$ 的水果數量和
  • 最後一次卸貨產生的銷售費用為 $Ns_i$
  • 水果 $k+1$ 至 $i$ 產生的積載費用為 $N(p_1 + p_2 + \ldots + p_i)$
  • 此次卸貨，在此城市將賣出 $r_{i, k+1} + r_{i, k+2} + \ldots + r_{i, i}$ 顆水果

可以注意到上面的轉移式中，$n, s, p, r_i$ 的和都可以用前綴和來 $O(1)$ 求出。因此只要輸入時先預處理這些數列的前綴和，便可以做到狀態 $O(cT)$ 轉移 $O(c)$ 的 DP，時間複雜度為 $O(c^2T)$。

滿分做法

因為 $T$ 的範圍太大不適合拿來當狀態，只好試著想辦法用水果數量來構造對偶狀態。考慮 DP 狀態 $\text{dp}[i][j]$：

  • $i$ 是最後一次卸貨給盤商銷售的城市（$=$ 賣出最大的水果種類）
  • $j$ 是到城市 $i$ 為止前 $i$ 種類水果銷售數量和
  • $\text{dp}[i][j]$ 為最後一次在城市 $i$ 卸貨，前 $i$ 種水果銷售量 $j$ 時所花的最小成本
  • 特殊地，若 $i=0$ 則代表尚未卸貨

轉移和上面 $O(c^2T)$ 的作法極為類似，分別列出每次卸貨所產生的積載、銷售成本以及銷售量轉式會很清楚因此就不多加贅述了。答案為滿足 $\text{dp}[i][j]\le T$ 最大可能的 $j$。

整體的複雜度分析：

  • 水果數量為 $\sum n_i$ 個，狀態數 $O(c\sum n_i)$
  • 轉移 $O(c)$
  • 因此 DP 的時間複雜度為 $O(c^2\sum n_i)$

G. 鳳梨關稅 (pineapple)

給定一棵有根樹，一開始每條邊權重都是 $1$，處理下列兩種操作：

  1. 把某條邊的權重變 $0$。
  2. 詢問根節點到某一節點的權重和。

詢問數和節點數都是 $10^5$ 等級。

Subtask 2

Root 的度數為 $1$，且其他節點度數最多為 $2 \Rightarrow$ 給的樹是一條 path。

這筆 subtask 可以用一棵 BIT 或線段樹來維護每條邊的權重，詢問等價於求序列前綴和。複雜度是 $O(n\log n)$。

滿分做法

假設某筆詢問將邊 $(x, y)$ 由 $1$ 改成 $0$，其中 $x$ 是父節點。這個操作相當於將子樹 $y$ 的答案都減 $1$。每次的操作都是一個子樹操作，因此我們可以先計算初始答案，並將樹的時間戳記用來做線段樹的 index，即可在每次操作 $O(\log n)$ 的時間維護訊息。這個技巧一般被稱作 Euler Tour Technique 或者俗稱樹壓平。對此技巧不熟悉的可以在上面連結或相關關鍵字找到資料。

H. 天竺鼠遊行 (puipui)

對於一個數列 $\mathbf{a} = a_1, a_2, \ldots, a_k$，定義 $f(\mathbf{a})$ 為

\[\max_{1 \le i \le k} \left| a_{(i\operatorname{mod}k)+1} - a_i \right|.\]

上式和題目所求的環狀數列最大高度差等價。現在給定 $n$ 個數 $h_1, h_2, \ldots, h_n$，想要從裡面抓出 $p$ 個 $k$ 項的數列 $\mathbf{a_1}, \mathbf{a_2}, \ldots, \mathbf{a_p}$（當然我們有 $n\ge pk$）。請問

\[\max_{1\le i\le p}f(\mathbf{a_i})\]

的最小值是多少？

Subtask 2: $k=n, p=1$

不失一般性，假定 $h_1 \le h_2 \le \ldots \le h_n$。經過亂嘗試以後我們發現似乎只要把奇數項從小排到大，再把偶數項從大排到小，就能給出最佳解。（至於為什麼亂試會得到這個結論，就留給讀者自行思考了 [窩不知道.jpg]）

為了接下來的討論方便，以下給出一些定義：

  1. 一個 $\sigma \in S_n$ 是 $1, 2, \ldots, n$ 的排列，我們寫成 $\sigma = \sigma(1), \sigma(2), \ldots, \sigma(n)$， 一個例子是 $\sigma = 1, 3, 5, 4, 2$。
  2. $\sigma|_i$ 為「從 $\sigma$ 去掉所有 $>i$ 的數後得到的 $1, 2, \ldots, i$ 排列」。例如當 $\sigma = 1, 3, 5, 4, 2$ 時，$\sigma|_3$ 就是 $1, 3, 2$。
  3. 對於所有的 $\tau \in S_i$，定義 $g(\tau; \mathbf{h})$ 為 \[\max_{1 \le j \le i} \left| h_{\tau((j\operatorname{mod}i)+1)} - h_{\tau(j)} \right|.\] 白話一點解釋，$g(\tau; \mathbf{h})$ 代表的是將前 $i$ 隻老鼠以 $\tau$ 排成環狀數列所得的最大高度差。 在本 subtask 中，我們要找出 $\sigma \in S_n$ 使得 $g(\sigma; \mathbf{h})$ 有最小值。
  4. 定義 \[\sigma^* = \begin{cases}1, 3, \ldots, n-2, n, n-1, n-3, \ldots, 2,&\text{if }n\text{ is odd},\\1, 3, \ldots, n-3, n-1, n, n-2, \ldots, 2,&\text{if }n\text{ is even}.\end{cases}\]

我們用數學歸納法證明 $\sigma^*$ 會給出最小的 $g(\sigma; \mathbf{h})$。對於 $n \le3 $，$g(\sigma; \mathbf{h}) = h_n - h_1$，在 $n$ 是 $3$ 以下的情況確實為最佳解。若 $n \ge 4$ 並考慮把 $n$ 插入 $\sigma^*|_{n-1}$ 以得到 $\sigma^*$ 的過程。由於 $n$ 被插入 $n-2$ 和 $n-1$ 中間且 $n-1$ 和 $n-3$ 相鄰，我們知道

\[g(\sigma^*|_{n-1}; \mathbf{h}) \ge h_{n-1} - h_{n-3} \ge h_{n-1} - h_{n-2}.\]

另一方面，對於任意 $\sigma \in S_n$，我們本來就有

\[\begin{cases} g(\sigma; \mathbf{h}) \ge h_n - h_{n-2},\\g(\sigma; \mathbf{h}) \ge g(\sigma|_{n-1}; \mathbf{h}).\end{cases}\]

所以可以分兩種情況：

  1. $g(\sigma^*|_{n-1}; \mathbf{h}) < h_n - h_{n-2} \Rightarrow g(\sigma^*; \mathbf{h}) = h_n - h_{n-2}$，故 $\sigma^*$ 為最小的 $g(\sigma; \mathbf{h})$。
  2. $g(\sigma^*|_{n-1}; \mathbf{h}) \ge h_n - h_{n-2} \Rightarrow g(\sigma^*; \mathbf{h}) = g(\sigma^*|_{n-1}; \mathbf{h})$，根據歸納法假設知道 $\sigma^*$ 也會最小化 $g(\sigma; \mathbf{h})$。

只要先將 $\mathbf{h}$ 排序好，就能在 $O(n)$ 時間內得出答案，時間複雜度為 $O(n\log n)$。

Subtask 3: $p = 1$

一樣先將 $\mathbf{h}$ 排序好，接著再用 sliding window 在 $O(n)$ 時間內得出答案，時間複雜度與 subtask 2 相同。

滿分做法

直接對答案 $x$ 做二分搜，判斷是否能切出 $\ge p$ 個 $k$ 項的數列 $\mathbf{a}$ 滿足 $f(\mathbf{a})\le x$。時間複雜度為 $O(n\log n + n\log H)$，其中 $H$ 是 $h_i$ 的最大值。

I. 鐵路鋪設 (rail)

給定 $L$，問 $2\times L$ 方格能放幾個不相交的迴圈使得所有方格中心都被經過，且每個迴圈最多只能有 $1$ 條斜邊。

令 $D_i$ 為 $L=i$ 時的方法數。對於任何一張合法的圖，我們從左邊到右邊找出第一個不會切到迴圈的鉛直線：

可以發現若鉛直線切出的寬度是 $l$ 與 $i-l$，則被切出 $l$ 的那邊有 $2l - 3$ 種填滿的方式，這樣一來我們就有

\[D_i = \sum_{j=0}^{i-2} (2(i-j)-3) D_j.\]

Subtask 1: $L\le7$

直接帶入遞迴式計算，時間複雜度是指數級。

Subtask 2: $L\le1000$

根據前面所介紹的遞迴式依序計算 $D_0, D_1, \ldots, D_L$，並用一個 DP 表格記錄算過的 $D_i$ 們，需時 $O(L^2)$。

Subtask 3: $L\le10^5$

整理遞迴式

\[\begin{split} D_i &= \sum_{j=0}^{i-2}(2(i-j)-3)D_j \\&= \sum_{j=0}^{i-2} (2i-2j-3) D_j \\&= (2i-3) \sum_{j=0}^{i-2} D_j - 2 \sum_{j=0}^{i-2} j D_j.\end{split}\]

令 $A_i := \sum_{j=0}^i D_j$ 以及 $B_i := \sum_{j=0}^i j D_j$，則上式可以進一步寫成

\[A_i - A_{i-1} = (2i-3) A_{i-2} - 2B_{i-2}.\]

加上 $B_i = B_{i-1} + i(A_i-A_{i-1})$ 這個條件，即可在 $O(L)$ 時間內算出 $D_L = A_L - A_{L-1}$。

Subtask 4: $L\le10^{10}$

我們再度化簡遞迴式：

\[\begin{cases}D_i = (2i-3) \sum_{j=0}^{i-2} D_j - 2 \sum_{j=0}^{i-2} j D_j,\\D_{i-1} = (2i-5) \sum_{j=0}^{i-3} D_j - 2 \sum_{j=0}^{i-3} j D_j.\end{cases}\]

將兩式相減得到

\[\begin{split} D_i - D_{i-1} &= (2i-3)D_{i-2} + 2 \sum_{j=0}^{i-3} D_j - 2(i-2)D_{i-2} \\&= D_{i-2} + 2\sum_{j=0}^{i-3} D_j, \end{split}\]

因此

\[\begin{cases}D_i - D_{i-1} - D_{i-2} = 2 \sum_{j=0}^{i-3} D_j,\\D_{i-1} - D_{i-2} - D_{i-3} = 2 \sum_{j=0}^{i-4} D_j.\end{cases}\]

再度將兩式相減得到

\[D_i - 2D_{i-1} + D_{i-3} = 2D_{i-3},\]

故有

\[D_i = 2D_{i-1} + D_{i-3}.\] 這是個線性遞迴式。搭配初始條件 $D_0 = 1, D_1 = 0, D_2 = 1$，則對於所有的 $L \ge 3$，皆有 \[\begin{pmatrix} D_L \\\ D_{L-1} \\\ D_{L-2} \end{pmatrix} = \begin{pmatrix} 2 & 0 & 1 \\\ 1 & 0 & 0 \\\ 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} D_{L-1} \\\ D_{L-2} \\\ D_{L-3} \end{pmatrix} = \begin{pmatrix} 2 & 0 & 1 \\\ 1 & 0 & 0 \\\ 0 & 1 & 0 \end{pmatrix}^{L-2} \begin{pmatrix} 1 \\\ 0 \\\ 1 \end{pmatrix}. \] 利用快速冪，即可在 $O(\log L)$ 時間內得出答案。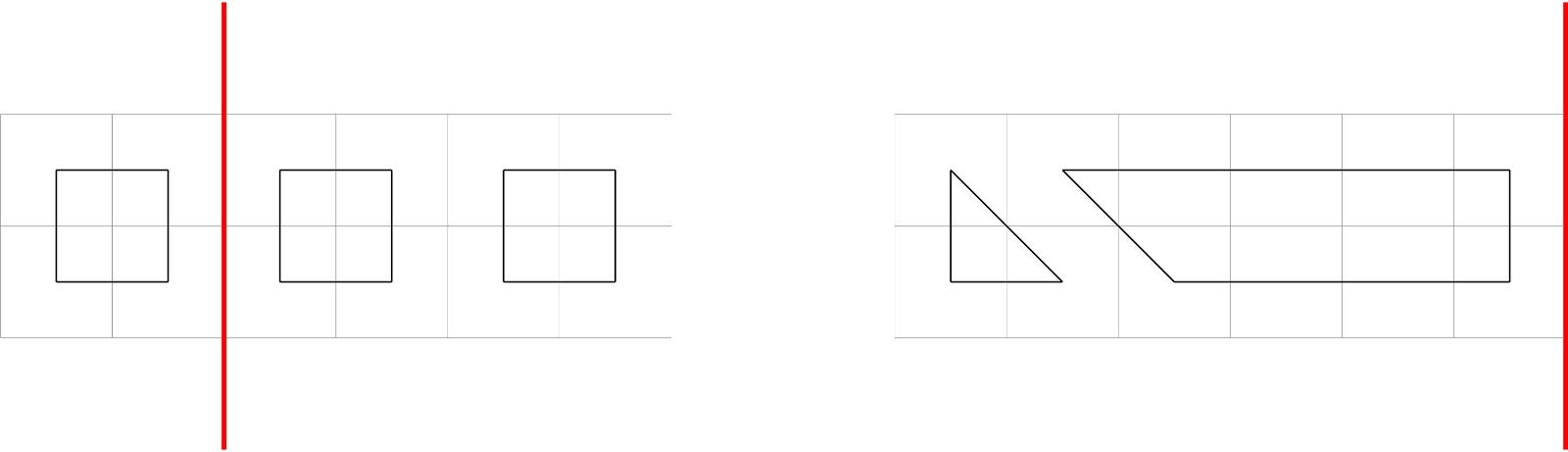

留言

張貼留言

這個網誌中的熱門文章

2020 全國賽驗題心得

筆者參與了本屆全國賽的驗題。驗題工作包含修正題目敘述與訂定時間限制，並 總是要 於必要時重出測試資料，前後花了一個多月才完成。讀者可以把這篇文章當作上篇 題解 的幕後花絮，簡單了解比賽題目是怎麼產生的，以及有哪些有趣的事情發生。由於筆者花最多時間在驗 pG 上，pG 會佔大部分的篇幅，還請見諒。 A. 礦砂採集 由於排序的 $\Theta(n\log n)$ 和 quickselect 的 $O(n)$ 以比賽來說難以區分，一開始就只預期參賽者用排序 AC。一度想過是否把 $n$ 的上限拉到 $10^5$ 卡 $\Theta(n^2)$ 排序，想說這題就是個簽到題就算了，可惜仍有參賽者未能拿到滿分。 B. 村莊與小徑 看到 scoreborad 有人卡在最後一個 subtask，有點好奇究竟是單純的 bug 還是堅信 SPFA 的時間複雜度是 $O(kE)$ 而狂傳。大概在 $10$ 年前，筆者還在打 TOI 的時候，簡體中文網路上就流傳著 SPFA 時間複雜度只有 $O(2E)$，快到可以作為 general 最短路徑演算法的都市傳說。筆者並不清楚為什麼許多中國人認為 Dijkstra 比 SPFA 難寫（筆者覺得正好相反）導致即使可能 TLE 也要寫 SPFA，不過總之請記得，如果一個題目能用 DAG 上 DP 或 Dijkstra 過，請不要用 SPFA。 C. 樣本解析 這題的交集關係部分寫得很繁瑣，但我們沒有辦法。本來打算用 $\subset$ 表示 proper subset，實際上也有 $\subseteq$ 這個符號，筆者認為就像 $<$ 和 $\leq$ 一樣，不應有混淆的空間；然而偏偏有些作者在用「$A \subset B$」時，允許 $A = B$，可能導致參賽者混淆而放棄。也考慮過改用 $\subsetneq$ 符號，但這跟 $\lneq$ 一樣相對罕見，考慮參賽者都是高中生很可能看不懂，只好全部改用中文敘述。 D. 水果包裝 筆者第一次看到題目後，在紙上推敲了許久（$30$ 分鐘有）才得出 greedy 結論，很意外這題的答題狀況這麼好 ，好奇到底有多少人是用猜的 。不過有一等獎參賽者沒能拿到滿分，用心出 $n$ 的數量級 $10^5$ 的測資也有了價值 (? 原先這題 $n$ 的上限只到 $100...
閱讀完整內容

水母上 Divide-and-Conquer

圖片
一棵樹有「拔掉任一非葉節點便不連通」的良好性質，可以幫助我們用 DP 和 divide-and-conquer 解決問題，例如 POJ 1741 和 TIOJ 1647 。這篇假定你知道怎麼把 POJ 1741 做到 $O(n(\log n)^2)$ 的時間複雜度 (如果你不知道也沒關係，google "POJ 1741" 就有很多資料了 XD)。我們沿用 先前 的定義，把一張點數和邊數相等的連通近圖 ( pseudograph ) 稱作一隻水母。再次提醒，水母並不是正式名稱 (我找不到正式名稱 orz)。 考慮這個問題：給定一隻大小為 $n$ 的水母 $J = (V, E)$，邊有正權重，請求出 $J$ 的 $K$-近對個數。一個 $K$-近對的定義是距離不超過 $K$ 的 (無序) 點對。觀察到一隻水母其實是由頭部 (環) 和數條觸手 (樹) 組成。設頭部由點 $t_0, t_1, \ldots, t_{m-1}$ 組成，從 $t_i$ 長出的觸手為 $T_i$。我們把 $K$-近對 $(u, v)$ 分成兩種：$u, v$ 屬於同一條觸手 ($\alpha$ 型)、$u, v$ 屬於不同條觸手 ($\beta$ 型)。只要在每條觸手上跑 POJ 1741，就能求出 $\alpha$ 型 $K$-近對個數了。至於 $\beta$ 型，做法是對於每個點 $v$，統計有幾個點 $u$ 滿足 $u$ 和 $v$ 不在同一條觸手上 $u, v$ 的距離 $d(u, v) \leq K$ 我們用上圖來做說明。設邊 $(t_i, t_{i+1})$ 的權重為 $w_{i+1}$，$s_i := w_1 + \ldots + w_i$ 為「從 $t_0$ 開始，順著 $t_0, t_1, t_2, \ldots$ 的方向，走 $i$ 條邊的里程數」(為了方便，不該超過 $m-1$ 的那些索引值，一旦超過 $m-1$ 就自動對 $m$ 取模)。設 \[ \begin{cases} u \in T_j, d_u := d(u, t_j),\\ v \in T_i, d_v := d(v, t_i), \end{cases} \] 則 $d(u, v)$ 就是 $d_u+d_v+(s_i-s_j)$?! 當然我們沒有這麼好的事情，因為 有...
閱讀完整內容

109 學年度全國資訊學科能力競賽各題詳解

筆者參與了這屆全國賽的驗題，也出了 pD 與 pG 的所有測試資料。由於現場講解有些不夠明確 ，故在這邊放一份兩位驗題者與筆者提供的詳解。題本的連結在 這裡 ，pE / pF / pG / pH 的時間限制分別為 2.0s / 2.3s / 6.5s / 0.1s，其餘題目皆為 1.0s。 A. 礦砂採集 這題是很典型的 連續背包問題 。結論非常簡單：只要不斷貪婪地將單位重量價值最大的礦砂放進背包，直到背包已滿或所有礦砂均已被放入，就能最大化總價值。 一個簡單的做法是將所有礦砂依照單位重量價值由大到小排序，依序放入背包直到滿即可。複雜度是 $O(n \log n)$。 線性做法 雖然並不是本題的考點，但有一個值得一提的 $O(n)$ 做法存在。以下為了方便說明，假定所有的 $x_i$ 均相異。 隨機選擇一個礦砂 $i$，並將所有的礦砂分為單位價值 $\ge x_i$ 與 $< x_i$ 兩堆。 分歧判斷： 若單位價值 $\ge x_i$ 的礦砂可以塞滿背包，則將 $< x_i$ 的礦砂全刪除，並往大的 $x$ 找答案。 反之則將價值 $\ge x_i$ 的礦砂全刪除，往小的 $x$ 找答案。 搜尋完後得到的值代表「總價值最大時，背包中單位重量價值最小的礦砂」，再用這個價值去反求答案。 演算法與 quickselect 非常相似，期望時間複雜度為 $O(n)$。 B. 村莊與小徑 這題是一道最短路徑的問題，但給定的限制中有幾個點要注意： 給定的圖是 DAG（有向無環圖）。 邊權可能是負的。 條件 1 保證這張圖存在拓樸排序，求解可用 top-down DP，或找出拓樸排序後用 bottom-up DP。 // ord = 拓樸排序的點順序 // fr[x] = 連到 x 的所有點 fill(dis, dis+n+ 1 , INF); dis[ 1 ] = 0 ; for ( int i= 1 ; i<=n; i++) { int p = ord[i]; // 找所有能連到 p 的點 j，更新 p 的最短距離 for (Edge j: fr[p]) dis[p] = m...
閱讀完整內容