TIOJ 1852 分眼皮

Description

你有 $n$ 張眼皮和三隻向姊，每張眼皮有他的角動量。
你希望把這些眼皮全部分給三隻向姊，為了避免眼皮爆走，所以需要讓向姊間的角動量差最小，否則向姊們就會吵架！
(假設所有眼皮轉動方向都是逆時針方向，且對於每隻向姊，她的所有眼皮的旋轉中心都相同)

Input Format

第 $1$ 行有一個數字 $n\ (3\leq n\leq24)$，代表眼皮的個數。
第 $2$ 行有 $n$ 個數字 $a_1, \ldots, a_n$，$1\leq a_i\leq10^9$，代表每張眼皮的角動量。

Output Format

輸出一個數字，代表角動量最大的向姊和角動量最小的向姊間的角動量差的最小值。

Sample Input

4
5 4 7 6

Sample Output

3

Solution

如果今天只有兩隻向姊，怎麼做呢？利用 meet-in-the-middle algorithm，可以做到 $O(n2^{n/2})$ 的時間複雜度，比 naïve 演算法的 $O(2^n)$ 快。以下將介紹怎麼在有三隻向姊的情況下，同樣利用 meet-in-the-middle 的精神，在 $O(n3^{n/2})$ 時間內求出答案。為了後續的討論方便，我們允許某個 $a_i \leq 0$，且允許某隻向姊沒分到任何眼皮。

假定三隻向姊拿到的眼皮角動量總和分別為 $p, q, r$，不失一般性令 $p \leq q \leq r$，目標最小化 $r-p$。設 $s := a_1 + \ldots + a_n$，則以下的兩個敘述至少一個會成立：

1. $p \leq q \leq s/3 \leq r$
2. $p \leq s/3 \leq q \leq r$

如果我們知道怎麼算出第一種情況 $r-p$ 的最小值，只要把每個 $a_i$ 變號，第一種情況 $r-p$ 的最小值就變成「變號前的第二種情況 $r-p$ 的最小值」了。接下來我們專注在「在限制 $p \leq q \leq s/3 \leq r$ 下最小化 $r-p$」上。

將 $a_1, \ldots, a_n$ 分成兩堆，$A = \{a_1, \ldots, a_{\lfloor n/2\rfloor}\}$ 和 $B = \{a_{\lfloor n/2\rfloor+1}, \ldots, a_n\}$ (這裡 $A$ 和 $B$ 都是 multiset)。對 $A$ 和 $B$，各自枚舉有哪些眼皮分給第一隻和第二隻向姊，時間複雜度 $O(n3^{n/2})$ (或 $O(3^{n/2})$，如果你要優化它的話 XD)。假定有一種選法，第一隻和第二隻向姊分別在 $B$ 中拿了角動量總和為 $\xi$ 和 $\eta$ 的眼皮。設兩隻向姊分別在 $A$ 中拿了角動量總和為 $x$ 和 $y$ 的眼皮，則根據 $p \leq q \leq s/3$，有 $$\begin{equation}\label{region} \begin{cases} y \leq s/3-\eta,\\ x \leq y+\eta-\xi. \end{cases} \end{equation}$$ 注意 $(\ref{region})$ 其實就是下圖的陰影部分 $K(s/3-\xi, s/3-\eta)$，包含邊界：

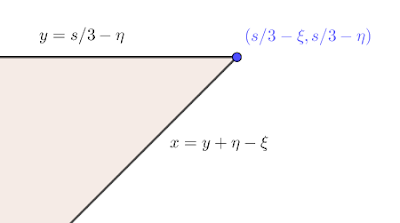兩隻向姊只能拿陰影部分的 $(x, y)$。

另一方面，固定 $(\xi, \eta)$，則 $r-p$ 的最小值就是 $$\begin{split} \min\{r-p\} &= \min\{(s-p-q)-p\}\\ &= \min\{s-2p-q\}\\ &= \min\{s-2(\xi+x)-(\eta+y)\}\\ &= s-2\xi-\eta-\max\{2x+y\}. \end{split}$$ 所以問題就被轉成：給定 $\mathbb{R}^2$ 上 $N := 3^{\lfloor n/2\rfloor}$ 個點 $P := \{(x_i, y_i)\}_{i=1}^N$，其中 $(x_i, y_i)$ 有權重 $w_i := 2x_i+y_i$。現在有 $M := 3^{\lceil n/2\rceil}$ 筆詢問 $\{(x_i', y_i')\}_{i=1}^M$，對詢問 $(x_i', y_i')$ 要回傳 $P\cap K(x_i', y_i')$ 裡的最大權重 (如果不存在則回傳 $-\infty$)。這個問題可以用一條斜率為 $1$ 的掃描線 (sweep line) 搭配 BIT (binary indexed tree) 做到 $O((N+M)\log N) = (n3^{n/2})$ 的時間複雜度，也就是整體的時間複雜度是 $O(n3^{n/2})$。

藍點為 $N$ 筆資料，紅點為 $M$ 筆詢問。往右移動橘色這條掃描線，記錄每個藍點 $y$ 值目前遇到的最大權重，並建立 BIT 來支援 $O(\log N)$ 查詢與修改。

這個題目問的是向姊有三隻的情形。如果向姊變成四隻，該怎麼做呢？好問題，我也不知道 wwwwww

我的 code：

https://ideone.com/CMTdMh

然後聽說這題的官方解法是爆搜 + 剪枝，囧。

(2018-05-04 補記)

想想後發現其實不需要討論 $q$ 和 $s/3$ 的大小關係。由 $p \leq q$ 和 $q \leq s-p-q$，固定 $(\xi, \eta)$，則兩隻向姊在 $A$ 中能拿到的 $(x, y)$ 區域變成 $$K'(\xi, \eta) := \{(x, y) \in \mathbb{R}^2: x-y \leq \eta-\xi, x+2y \leq s-\xi-2\eta\}.$$ 注意 $$K'(\xi, \eta) = \left\{\begin{pmatrix}\frac{s}{3}-\xi\\\frac{s}{3}-\eta\end{pmatrix}+\alpha\begin{pmatrix}2\\-1\end{pmatrix}+\beta\begin{pmatrix}1\\1\end{pmatrix}: \alpha \leq 0, \beta \leq 0\right\}.$$ 因此只要一個座標變換，就能用垂直掃描線和 BIT 做到 $O(n3^{n/2})$ 的時間複雜度，詳細部分可以直接參考我的 code：
https://ideone.com/7u8TS2

這個方法可以推廣到向姊有 $k\ (k \geq 4)$ 隻的情況，時間複雜度是 $O(n^{k-2} k^{n/2})$，不過實作上很麻煩 (我的方法要用到 $k-2$ 層的 binary search tree)，又不怎麼實用 orz。