TIOJ 1670 新聞採訪

Description

「我與小明不相見已有二年餘了，我最不能忘記的是他的雙腿。（雖然他根本沒有）」

光陰荏苒，你如今是一位御用新聞記者，專門替國王烏龜的電視台採訪各式各樣的新聞。還記得TIOJ 1623--國王烏龜的接駁車嗎？大意就是國王烏龜開放死老百姓烏龜們去覲見國王，舉國上下無不歡聲雷動，一時之間各個直達皇宮接駁車的站牌前都排滿了烏龜，好不盛大！你自然被派遣過去負責採訪這場盛宴。並且他們看在你的才能，決定要讓你Live連線報導，你知道如果把這個難得的機會搞砸了你可能會變成小明第二。

因此，在開始報導之前你決定先去向前輩烏龜瞭解你的報導方式。

「
你待會要進行的報導方式呢，你看那邊有一條大排長龍的隊伍，共有 $n$ 隻烏龜排成一列，你需要選擇一個區間 $[A, B]$（包含$A, B$）進行採訪，採訪的方式是依序遞麥克風給這個區間每一隻烏龜，讓他們自由發言。必須注意的是因為要弄得看起來很有公信力，你採訪的總人數不能小於 $L$ 個人。

當然自由發言是有危險成份在的，有些反國王份子可能會講出危言聳聽的話，危害國王聲譽，所以我們會依序把烏龜標號 $0$ 或 $1$，$0$ 表示危險份子、$1$ 則是很安全。

所以，我們希望你能讓這個區間內 $\mathbf{1}$ 佔的比例越大越好，如果有很多個一樣好的區間，那就是總人數越少越好（但還是得 $\geq L$），如果還是有很多個，那就 $A$ 越小越好。

你選好你要採訪的區間了嗎？告訴我吧。
」

Input Format

輸入第一行含一個正整數 $T$，表示接下來有幾條隊伍要採訪（幾組詢問）

每組詢問第一行含兩個正整數 $n, L$（$L \leq n$），分別表示隊伍長度跟採訪總人數下限。

第二行會是一個長度為 $n$ 的 $01$ 序列，依序表現出每隻烏龜危不危險。

• $T \leq 400$
• $1 \leq n \leq 100,000$

Output Format

對每組詢問輸出兩個正整數數字 $A$ 和 $B$，表示 $[A,B]$ 是你的最佳選擇。

※這個序列編號由 $1$ 開始，到 $n$ 為止。

Sample Input

2

17 5

00101011011011010

20 4

11100111100111110000

Sample Output

7 11

6 9

Solution

我們考慮更一般的情形：給定 $a_1, a_2, \ldots, a_n \in \mathbb{R}$ 和 $1 \leq k \leq n$，找出 $[l, r] \subseteq [0, n]$ 在限制 $r-l \geq k$ 下最大化 $$f(l, r) := \frac{\sum_{i=l+1}^ra_i}{r-l}$$ 為了方便，對於每個 $i \geq k$，定義

1. $F(i) := \max_{0 \leq j \leq i-k}f(j, i)$。
2. $j^*(i)$ 為最大的 $j$ 使得 $f(j, i) = F(i)$。
3. $G(i) := \max_{k \leq i' \leq i} F(i')$。

接著，考慮 $s_i := \sum_{j=1}^i a_i$ 與 $P_i := (i, s_i) \in \mathbb{R}^2$。這樣一來就有 $$f(l, r) = \frac{s_r-s_l}{r-l} = m(P_l, P_r)$$ 這裡 $m(P, Q)$ 代表線段 $\overline{PQ}$ 的斜率。不難發現 $P_{j^*(i)}$ 必定在 $P_0, \ldots, P_{i-k}$ 形成的下凸包邊界 $C_{i-k}$ 上。設 $C_{i-k}$ 包含了 $c_{i-k}$ 個點，由左到右分別是 $C_{i-k, 1}, \ldots, C_{i-k, c_{i-k}}$，且 $P_{j^*(i)} = C_{i-k, j^{**}(i)}$，則我們有 $$\begin{equation}\label{squeeze}m(C_{i-k, j^{**}(i)-1}, C_{i-k, j^{**}(i)}) \leq F(i) = m(P_{j^*(i)}, P_i) < m(C_{i-k, j^{**}(i)}, C_{i-k, j^{**}(i)+1})\end{equation}$$

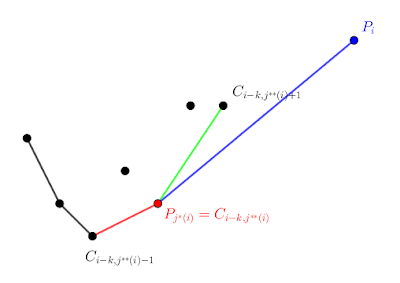$P_{j^*(i)}$ 必定在下凸包邊界 $C_{i-k}$ 上，且藍色線段的斜率會在紅色和綠色線段的斜率之間。

回想一下，$C_0, \ldots, C_{n-k}$ 能用 Andrew's 演算法在 $O(n)$ 時間內依序做出來。只要對每個 $i \geq k$，在 $C_{i-k}$ 上做二分搜找出 $j^{**}(i)$，就能在 $O(n\log n)$ 時間解決這個問題。不幸的是，因為這題的 $T$ 頗大，$O(n\log n)$ 還是太慢。

以下介紹一個將時間複雜度降至 $O(n)$ 的演算法。假定我們有一個指標 $1 \leq p \leq c_{i-k}$，滿足 $$\begin{equation}\label{pp}m(C_{i-k, p-1}, C_{i-k, p}) \leq G(i)\end{equation}$$ 為了方便，如果 $p=1$，定義 $m(C_{i-k, p-1}, C_{i-k, p}) = -\infty$。
首先，若 $C_{i-k, p} \notin C_{i-k+1}$，則把 $p$ 重設為$c_{i-k+1}-1$。注意無論 $p$ 是否被重設，我們都有 $C_{i-k+1, p-1} = C_{i-k, p-1}$ 且 $C_{i-k+1, p} = C_{i-k, p}$，因此 $$m(C_{i-k+1, p-1}, C_{i-k+1, p}) = m(C_{i-k, p-1}, C_{i-k, p}) \leq G(i).$$

假定加入 $P_{i-k+1}$ 後，$C_{i-k, p}$ 被 pop 掉，則往左移動 $p$ 至 $C_{i-k}$ 與 $C_{i-k+1}$ 最右邊的共同點 $p'$。注意紅色斜率 $<$ 粉紅色斜率，且根據假設粉紅色斜率 $\leq G(i)$，所以紅色斜率 $\leq G(i)$。

接著，在 $C_{i-k+1}$ 上，往右移動 $p$ 直到 $p$ 碰到右邊界或 $m(C_{i-k+1, p}, C_{i-k+1, p+1}) > m(C_{i-k+1, p}, P_{i+1})$。如果 $j^{**}(i+1) \geq p$，這麼做會把 $p$ 更新為 $j^{**}(i+1)$，也能求出 $F(i+1)$ 以及 $j^*(i+1)$，且由 $(\ref{squeeze})$ 可得 $$m(C_{i-k+1, p-1}, C_{i-k+1, p}) \leq F(i+1) \leq G(i+1)$$ 注意上式其實就是用 $i=i+1$ 代入 $(\ref{pp})$ 的結果。

如果 $j^{**}(i+1) \geq p$，向右移動 $p$ 至 $p'$ 後會得到 $p' = j^{**}(i+1)$。注意移動結束後藍色斜率 $F(i+1) \geq$ 紅色斜率 $m(C_{i-k+1, p'-1}, C_{i-k+1, p'})$。

如果 $j^{**}(i+1) < p$，這麼做並不會改變 $p$。由 $(\ref{squeeze})$，我們依然有 $$F(i+1) < m(C_{i-k+1, p-1}, C_{i-k+1, p}) \leq G(i) = G(i+1)$$ 在這種情況下我們沒辦法知道 $F(i+1)$ 是多少，但因為 $F(i+1) < G(i)$，$F(i)$ 是多少其實根本不重要。
有了上述的討論，只要在 $i=k$ 時設 $p = 1$，接著從 $i = k+1$ 做到 $i=n$，$p$ 的總移動次數將是 $O(n)$，因此時間複雜度也是 $O(n)$。

講起來似乎很複雜，其實 code 蠻簡單的：
https://ideone.com/ifDKHH