TIOJ 1317 統治世界 Reign

4月 30, 2018

Description

hellogameboy 正在進行一個神秘的計畫
他打算以 H 的力量來征服全世界，讓世界都屈服在他的 H 勢力之下
這時候正義的 hallogameboy 挺身而出，決心鼎力維持這個世界的正直

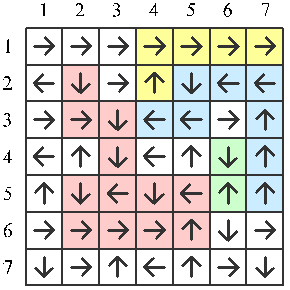
想像這世界是一個

$n\times n$ 的格子棋盤，每個格子都是一個城市
而時事潮流總有固定的流向，因此對於每個格子都有一個"潮流傳播方向" (上、下、左、右之一)
若某個城市的潮流是流向棋盤邊界外，當然，這個城市的潮流就不會傳播給任何人

hellogameboy 和 hallogameboy 將輪流展開行動，
由 hellogameboy 先展開 H 的攻勢，再換 hallogameboy 進行正直防守......
攻防不斷交替地進行，直到所有城市都被佔領

一開始所有城市都是純潔的，沒有受到任何佔領
而 he(a)llohameboy 將選擇一個"源流城市"佔領
H (正直) 的力量就會從這個源流城市開始沿著每個格子的潮流傳播方向傳播
路上的城市都被佔領，直到某個潮流傳出邊界，或是遇到某個已被佔領的城市才停止。

以上圖為例（佔領攻防還沒結束，也不是最佳佔領策略）
hellogameboy 先選擇

$(2,2)$ ，並佔領紅色的

$12$ 格
再來換 hallogameboy，選擇

$(5,7)$ ，佔領藍色的

$8$ 格
再來又輪到 hellogameboy，選擇

$(5,6)$ ，佔領綠色

$2$ 格
hallogameboy 再選擇

$(2,4)$ ，佔領黃色等

$5$ 格……

給定一個地圖，假設 hallogameboy 和 hellogameboy 都是絕頂聰明的人物
那麼請問，最後 hellogameboy 將以 H 勢力會統領多少土地呢?

Input Format

第一行為一個整數

$n$ ，代表地圖邊長。
再來為

$n$ 行，每行是一個不含空白的字串，由 l、r、u、d 構成，依序代表左、右、上、下的箭頭。

$1\leq n\leq 2000$

Output Format

一個整數，代表先者 (hellogameboy) 可以佔領多少格。

Sample Input

6
drludl
rudlru
dldldl
rldlrd
uuudlr
ddlluu

Sample Output

Solution

設

$V$ 為這

$n^2$ 個格子的集合，

$f: V\to V$ 為潮流傳播函數，規定如果某個點

$v$ 流向

$u$ 或邊界，則

$f(v) = u$ 或

$f(v) = v$ 。用

$f$ 建立一張 functional graph

$F = (V, E)$ ，其中

$E = \{(v, f(v)): v \in V\}$ 。兩位玩家輪流在一局中選定一個點

$s$ ，令

$S$ 為「從

$s$ 出發能到達的點集合」，則在該局得到

$|S|$ 分，並執行

$F \gets F-S$ 。

為了方便，我們先定義一些名詞，儘管這些並不是正式名稱。我們定義一隻 (無向) 水母 ~~(jellyfish)~~ 為點數和邊數相同的連通近圖 (pseudograph)。一隻水母由一個頭部 (環)，以及從頭部上的每個點長出來的觸手 (樹) 組成。

一隻頭部大小為

$4$ 的水母，頭部上的每個點是每條觸手的根。

將一隻水母頭部的邊定向 (順時針或逆時針都可以)，並對每條觸手上的每條邊，規定邊的方向為父節點 (parent node) 到子節點 (child node)，得到總攻有向水母 ~~(seme directed jellyfish)~~。

將上面那隻水母的邊定向，得到總攻有向水母。

類似地，我們可以定義總受有向水母 ~~(uke directed jellyfish)~~；注意將一隻總攻有向水母上的每條邊反向後，就得到總受有向水母。

將上面那隻總攻有向水母的邊反向，得到總受有向水母。

這樣一來，任意 functional graph 都能被拆解成數隻總受有向水母。

回到「選擇一個點

$s$ ，把

$s$ 能到達的點集合

$S$ 拔掉」這個操作。假定

$s$ 在某隻總受有向水母

$J$ 上，則無論

$s$ 是多少，

$S$ 一定包含

$J$ 的頭部。我們可以把

$F$ 中的每隻水母的頭部縮成一個點，規定這個點的權重為頭部大小，而其他觸手上的點的權重為

$1$ 。這樣一來，原問題就被 reduce 成：給定總受有向森林

$G$ (i.e. 每條邊的方向都是子節點到父節點)，點有非負權重。兩位玩家輪流在一局中選擇一個點

$s$ ，並設

$s$ 能到達的點集合為

$S$ ，則該局的得分為

$S$ 的權重和，並執行

$G \gets G-S$ 。目標求出最佳策略下兩位玩家的得分。

不難發現，如果先手開局選擇某個頂點

$v$ 有策略可以在遊戲結束時拿

$t$ 分，則選擇任意

$v$ 的子孫 (descendant) 開局也有策略在遊戲結束時拿到至少

$t$ 分。所以我們可以在遊戲中加入一條規則：每回合選擇的點必須是葉節點 (leaf node)。這樣一來，遊戲進行一局，

$G$ 的葉子數量就少

$1$ 。

那麼先手該怎麼開局呢？有個簡單的貪婪 (greedy) 策略：選擇最大化第一局得分的葉子開局。我們先定義一些符號讓接下來的證明更加清晰：固定

$m \geq 1$ 並設

$H$ 為任意「有

$m$ 片葉子的總受有向森林」，我們說性質

$\mathcal{P}_m$ 成立，若且唯若對於所有的

$H$ ，開局貪婪會最大化最終分數。

現在固定

$H$ ，設貪婪策略選擇以

$H$ 的某片葉子

$v_1$ 開局，並在第一局拿到

$s_1$ 分，最終拿到

$S_1$ 分。假定先手改選擇

$v_2$ (可以等於

$v_1$ ) 開局，讓他在第一局拿到

$s_2$ 分，最終拿到

$S_2$ 分。以下是一個小引理：

[引理 A] 若 $\mathcal{P}_m$ 成立，則 $S_1 \leq S_2 + (s_1-s_2)$ 。

證明如下：把

$H$ 裡的

$v_2$ 權重增加

$s_1 - s_2$ 得到

$H'$ ，則根據

$\mathcal{P}_m$ ，我們知道在

$H'$ 上的遊戲，開局選擇

$v_1$ 和

$v_2$ 能獲得相同的最終分數。因為在

$H'$ 上，以

$v_2$ 開局的最終分數是

$S_2 + (s_1-s_2)$ ，而以

$v_1$ 開局的最終分數至少有

$S_1$ ，可知

$S_2 + (s_1-s_2) \geq S_1$ 。

[定理] 對於所有的 $m \geq 1$ ， $\mathcal{P}_m$ 均成立。

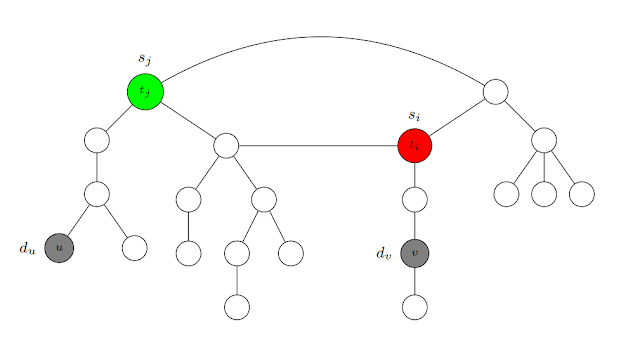
我們對

$m$ 做數學歸納法，並設

$G$ 為任意「有

$m$ 片葉子的總受有向森林」。當

$m=1$ 時，

$G$ 就是一條串列 (list)，而先手也只有一種選擇，自然是最佳的。假定

$m \geq 2$ ，不失一般性假定

$G$ 只有一棵樹 (否則加一個權重為

$0$ 的節點

$s$ ，並對

$G$ 裡的每個樹根

$r$ ，加入有向邊

$r\to s$ )。將葉子編號為

$v_1, v_2, \ldots, v_m$ ，並假設開局選擇

$v_1$ 能在第一局拿到最大分數

$s_1$ 。假定先手在開局選擇

$v_2$ 得到

$s_2$ 分，並使

$v_1$ 的分數降低成

$s_1^-$ ，而在這之後兩人認真玩遊戲。根據歸納法假設，可以假定兩人在第二局以後的每一局都選擇最大化該局得分的葉子。我們把這場遊戲每一局的策略與得分記錄下來：

$A(u_1:=v_2, t_1:=s_2) \to B(u_2, t_2) \to A(u_3, t_3) \to B(u_4, t_4) \to \ldots$ 注意我們有

$t_2 \geq t_3 \geq t_4 \geq\ldots$ 。設

$k\geq 2$ 是最小的整數滿足

$t_k \leq s_1^-$ (

$k$ 必定存在，因為有一局

$v_1$ 被選到，而那時選擇

$v_1$ 的得分必定不超過

$s_1^-$ )。為了方便，設

$v_1$ 和 $v_2$ 的 LCA (lowest common ancestor, 最低共同祖先) 為 $a$
從 $v_1$ 到 $a$ 的前一個節點為 $p$ (可能為 $v_1$ )
從 $v_2$ 到 $a$ 的前一個節點為 $q$ (可能為 $v_2$ )

則

$s_1^-$ 就是從

$v_1$ 到

$p$ 的點權重總和。注意對於所有的

$2 \leq i \leq k-1$ ，

$u_i$ 不可能是「以

$a$ 為根的子樹」的葉子，否則在開局選擇

$u_i$ 所獲得的分數就會超過

$s_1$ 。因此，在第

$k$ 局選擇

$v_1$ 的分數還是

$s_1^-$ ，由歸納法假設可以假定

$u_k = v_1$ ；另一方面，假設兩人重玩一次這個遊戲，且先手以

$v_1$ 開局後兩人認真玩遊戲，則在第

$2$ 到第

$k-1$ 局，根據歸納法假設，也可以假定玩家分別選擇

$u_2, \ldots, u_{k-1}$ 並拿到

$t_2, \ldots, t_{k-1}$ 分。

Case 1: $k$ 是奇數

在第二場遊戲中，先手只要在第

$k$ 局選擇

$v_2$ ，最終分數就能和第一場一樣，因此開局選擇

$v_1$ 不會比較差。

Case 2: $k$ 是偶數

設在第二場遊戲的第

$k$ 局，後手選擇

$u'_k$ (可以是

$v_2$ 或其他還沒被選到的葉子)。注意在這一局選擇

$u'_k$ 獲得的分數

$\sigma \leq s_1^-$ ，而選擇

$v_2$ 獲得的分數則是

$s_2^- := ($ 從

$v_2$ 到

$q$ 的點權重總和

$) \leq \sigma$ 。不妨設這一局，拔去「

$u'_k$ 到根的路徑」前的森林是

$H$ 。假設兩人第三次玩這個遊戲，其中前

$k-1$ 局的策略和第二次一樣，而在第

$k$ 局後手選擇

$v_2$ ，接下來兩人繼續認真玩遊戲。設第

$i\ (i = 1, 2, 3)$ 場遊戲的最終得分是

$S_i$ ，則由引理 A 我們有

$S_2 \geq S_3 - (\sigma - s_2^-) \geq S_3 - (s_1^--s_2^-) = S_1$ 因此開局選擇

$v_1$ 還是不會比較差。

注意

$G$ 可以是任意的，因此

$\mathcal{P}_m$ 對於所有的

$m \geq 1$ 都成立。

這個猜測和證明是我想的 ~~(因為當初 google 不到答案只好自己想了 QAQ)~~，如果有人能提出其他證明歡迎踢館。

至於實作部分，這題的記憶體限制非常緊，我連「用原本的 functional graph 建立總攻有向森林」都辦不到，吃了超多次 MLE。要看某個點的子節點們，只能每次看地圖上的上下左右四格，用時間換取空間。如果這題記憶體不要卡得這麼緊，優先權佇列 (priority queue) 可以用

$n^2$ 條 list 實作，做到

$O(n^2)$ 的時間複雜度。

以下是我的 AC code，時間複雜度

$O(n^2\log n)$ ，且除了 c++ 的 priority_queue 以外的地方都是

$O(n^2)$ 的：
https://ideone.com/H4nMwe

然後這是我第一次 AC 截的圖，為了不要 MLE 做了各種空間上的優化，真是辛苦我自己了 (無誤)：

搜尋此網誌

柊四千的倉庫