淺談大數除法 Part 1: 長除法
整數的加減乘除四種運算，無論是在國小算術或是在程式設計中，除法都比其他三種運算來得麻煩。舉例來說，假定我們想動手算 $1650794238\div 26451$，長除法的第一步是
我們必須猜出 $\Box$ 內要填的數字，而這正是除法計算痛苦的來源。因為我們沒有表可以查，只能猜一個數字 $\alpha$，放入 $\Box$ 中，看看 $165079 - 26451\alpha$ 是否介於 $0$ 到 $26450$ 之間，而如果不幸猜錯，還得重猜並重新計算一次乘法和減法。
我們把這個猜商問題寫得再清楚一點：給定兩個 $b$ 進位的整數 \[\begin{cases}\xi = x_{n-1}\ldots x_1x_0= x_{n-1} b^{n-1} + \ldots + x_1b + x_0,\\\eta = y_{n-1}\ldots y_1y_0= y_{n-1} b^{n-1} + \ldots + y_1 b + y_0,\end{cases}\] 其中
我們把這個猜商問題寫得再清楚一點：給定兩個 $b$ 進位的整數 \[\begin{cases}\xi = x_{n-1}\ldots x_1x_0= x_{n-1} b^{n-1} + \ldots + x_1b + x_0,\\\eta = y_{n-1}\ldots y_1y_0= y_{n-1} b^{n-1} + \ldots + y_1 b + y_0,\end{cases}\] 其中
- $0 \leq x_i \leq b-1$ 對於所有的 $0 \leq i \leq n-2$，而 $x_{n-1} \geq 0$ (可以超過 $b-1$，如上面的例子 $b=10, n=5$ 而 $a_4 = 16$)。
- $0 \leq y_i \leq b-1$ 對於所有的 $0 \leq i \leq n-1$，且 $y_{n-1} \neq 0$。
- $\lfloor\xi/\eta\rfloor \leq b-1$。
策略一：枚舉 $a = 0, 1, \ldots, b-1$
最糟情況猜商次數 $\Theta(b)$，不解釋。
策略二：在 $0, 1, \ldots, b-1$ 之間做二分搜找出 $a$
這是策略一的簡單改良，猜商次數 $\Theta(\log b)$，一樣不解釋。
策略三：利用 $x_{n-1}$ 和 $y_{n-1}$，縮小策略二的二分搜範圍
想法是這樣的：因為
\[\begin{cases}x_{n-1}b^{n-1}\leq\xi\leq(x_{n-1}+1)b^{n-1}-1,\\y_{n-1}b^{n-1}\leq\eta\leq(y_{n-1}+1)b^{n-1}-1,\end{cases}\]
我們知道
\[\lfloor\frac{x_{n-1}}{y_{n-1}+1}\rfloor \leq a \leq \lfloor\frac{x_{n-1}}{y_{n-1}}\rfloor\]
但不幸的是，如果 $y_{n-1} = 1$，二分搜的範圍大小在最糟情況還是 $\Theta(b)$，也就是猜商次數依然是 $\Theta(\log b)$。
策略四：看最高一位不夠，那你有看最高兩位嗎？
如果 $n = 1$，則 $a = \lfloor x_0/y_0\rfloor$ 本來就能直接計算 (如同小學算術中，$n$ 位數除以 $1$ 位數的商的每位數，都能從九九乘法表直接得到)。以下假定 $n \geq 2$：如果我們考慮 $X := x_{n-1}b + x_{n-2}, Y := y_{n-1}b + y_{n-2}$，利用策略三的想法，一樣有
\[\lfloor\frac{X}{Y+1}\rfloor \leq a \leq \lfloor\frac{X}{Y}\rfloor\]
因為
\[\frac{X}{Y} - \frac{X}{Y+1} = \frac{X}{Y(Y+1)} \leq \frac{b}{Y} \leq 1\]
我們發現 $\lfloor\frac{X}{Y+1}\rfloor$ 和 $\lfloor\frac{X}{Y}\rfloor$ 之間，最多只能包含 $2$ 個整數，因此無論 $b$ 是多少，在任何情況下都能在 $2$ 次內猜中 $a$。
有了上面的猜商策略四，設在 $b$ 進位表示下 $\xi$ 和 $\eta$ 的長度分別為 $n$ 和 $k$，則用長除法計算 $\lfloor\xi/\eta\rfloor$ 的時間複雜度就是 $O(kn)$，與 $b$ 無關。讀者可以在 ZJ c429 測試這個猜商策略。這個猜商策略給了我們一個啟示：如果我們小時候背的不是 $9\times 9$ 乘法表，而是 $99\times 9$ 乘法表，也許在計算除法時，就不會這麼痛苦了 XD
可能會有人問：大數除法有 $O(n\log n)$ 時間複雜度的演算法，那為什麼我還在這邊惹人嫌討論怎麼把 naïve 演算法寫好。我故意把時間複雜度寫成 $O(kn)$ 而不是 $O(n^2)$，其實是在暗示當 $k\ll n$ (但 $k$ 還是大到 $\eta$ 沒辦法用 long long 之類的變數型態裝下)，naïve 演算法的 $O(kn)$ 會比常數很大的快速除法 $O(n\log n)$ 快很多。順便一提，我測試了一下，發現 python 與 java 的內建大數並沒有對這種情況做特殊處理：用 python 與 java 的內建大數計算某個長度 $30$ 萬的整數除以 $2$ 的商，執行時間分別為 $1.6$ 和 $1.9$ 秒，超慢 wwwwww
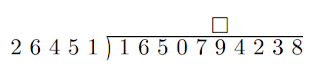
留言
張貼留言