發表文章

由14個點組成的5-正則圖必不是平面圖

圖片
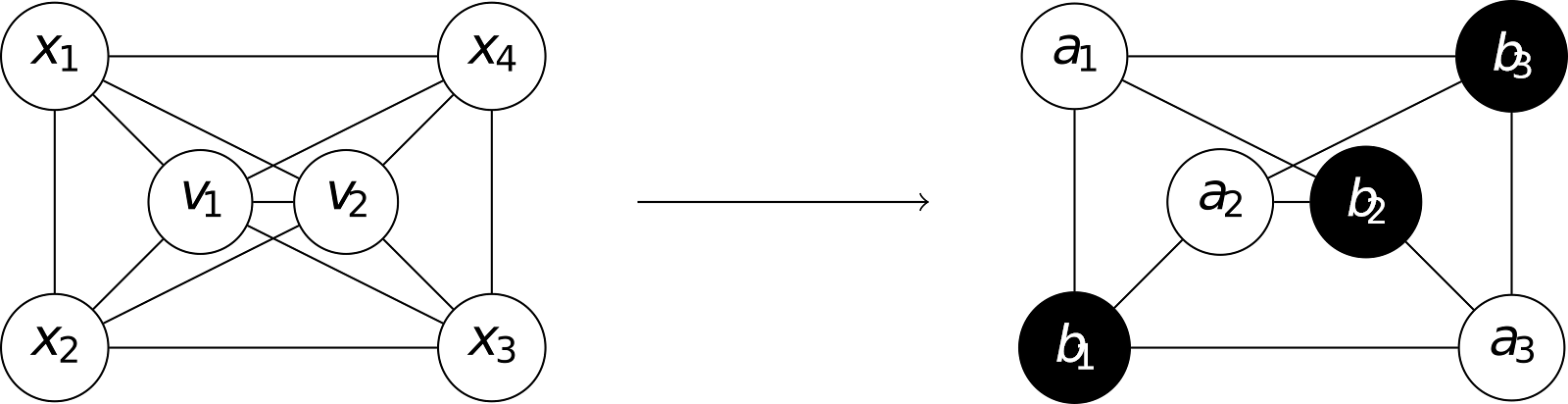
我們用反證法證明結論。假定存在 $5$-正則平面圖 $G_0$ 且 $|V(G_0)|=14$，不妨設 $G_0$ 已經嵌入(embed) $\mathbb{R}^2$ 裡了。首先觀察到 \[|E(G_0)| = \frac{1}{2} \cdot 5 \cdot 14 = 35.\] 另一方面，平面圖的邊數上限給出 $3|V(G_0)| - 6 = 36$，我們可以得到以下的引理： [引理 1] $G_0$ 恰包含一個 $4$ 邊組成的面 (face)。 我們加一條邊在 $G_0$ 唯一的 $4$ 邊組成的面，得到新的平面圖 $G$。$G$ 會滿足以下的性質： $G$ 有 $12$ 個點的度數為 $5$ 且有 $2$ 個點的度數為 $6$。 $G$ 上度數為 $6$ 的兩個點相鄰。 $G$ 的每個面都是三角形，且每條邊恰好夾在兩個面中間。 一個平面圖上的簡單環 $C$ 會將這個平面圖的點集合切成三塊：$C$ 內部的點 $V_\text{in}(C)$、$C$ 外部的點 $V_\text{out}(C)$、以及 $C$ 上的點 $V(C)$。我們有以下的兩個引理： [引理 2] $G$ 的每個三角形都是面。 假定引理為假，即 $G$ 有個三角形 $x_1x_2x_3$ 滿足 $|V_\text{in}(x_1x_2x_3)|$ 與 $|V_\text{out}(x_1x_2x_3)|$ 皆不為 $0$。 由於 $|V_\text{in}(x_1x_2x_3)| + |V_\text{out}(x_1x_2x_3)| = 11$，我們可以假設 $|V_\text{in}(x_1x_2x_3)| \le 5$。 另一方面，由於 $G$ 裡所有點的度數皆至少為 $5$，必須有 $|V_\text{in}(x_1x_2x_3)| \ge 3$。 情況 1：$|V_\text{in}(x_1x_2x_3)| = 3$ 由於對任意 $v \in V(G)$ 皆有 $\deg(v) \ge 5$，我們發現 導出子圖 (induced subgraph) $G[V_\text{in}(x_1x_2x_3)\cup\{x_1, x_2, x_3\}] \cong K_6$，包含了 $K_5$ 結
張貼留言
閱讀完整內容

110 學年度全國資訊學科能力競賽各題詳解

圖片
筆者這次也參與了全國賽的驗題，這邊放一份另一位驗題者與筆者提供的詳解。題本的連結在 這裡 ，pC / pE / pH / pI 的時間限制分別為 2.5s / 2.5s / 2.0s / 0.1s，其餘題目皆為 1.0s。另，讀者也能在 這裡 找到與下文基本相同的內容。 A. 髮廊服務優化問題 (barbershop) 有 $n$ 個人一起來店，第 $i$ 個人的服務時間為 $t_i$。每個客人等待時間是前面人 $+$ 自己服務時間總和，求等待時間總和的最小值。例如：三個人服務時間為 $2,1,3$，若服務順序為 $1,2,3$ 則等待時間總和為 $2 + (2+1) + (2+1+3) = 11$。 等價題序：給一個陣列 $\mathbf{t} := \{t_i\}_{i=1}^n$，將 $\mathbf{t}$ 重新排列使得 $nt_1 + (n-1)t_2 + (n-2)t_3 + \ldots + t_n$ 最小。由上式不難得知，順序越前面被乘的係數就越大，所以可以貪心地將數字從小排到大。複雜度 $O(n \log n)$。 B. 校園公車 (bus) 給定由 $n$ 條線段組成的折線 $\mathbf{P} := \left\{ \overline{P_i P_{i+1}} \right\}_{i=1}^n$ 與一點 $O$，問 $O$ 到 $\mathbf{P}$ 的最短距離。 先考慮這個問題：給定一線段 $\overline{PQ}$ 與一點 $O$，求 $O$ 到 $\overline{PQ}$ 的距離。首先我們作 $O$ 到 $\overline{PQ}$ 的垂足 $H$，並試著計算 $\overline{OH}$。注意 $\overline{OH}$ 其實就是 $\Delta OPQ$ 以 $\overline{PQ}$ 為底時的高，所以可以用下面的方法計算： Length_OH(O: Point, PQ: Segment): A ← ΔOPQ return 2A/|PQ| $\Delta OPQ$ 可以用 Shoelace formula 計算。 但事情沒有這麼簡單。$O$ 到 $\overline{PQ}$ 的距離並不總是 $\overline{OH}$：當 $\angle OPQ
張貼留言
閱讀完整內容

2020 全國賽驗題心得

筆者參與了本屆全國賽的驗題。驗題工作包含修正題目敘述與訂定時間限制，並 總是要 於必要時重出測試資料，前後花了一個多月才完成。讀者可以把這篇文章當作上篇 題解 的幕後花絮，簡單了解比賽題目是怎麼產生的，以及有哪些有趣的事情發生。由於筆者花最多時間在驗 pG 上，pG 會佔大部分的篇幅，還請見諒。 A. 礦砂採集 由於排序的 $O(n\log n)$ 和 quickselect 的 $O(n)$ 以比賽來說難以區分，一開始就只預期參賽者用排序 AC。一度想過是否把 $n$ 的上限拉到 $10^5$ 卡 $O(n^2)$ 排序，想說這題就是個簽到題就算了，可惜仍有參賽者未能拿到滿分。 B. 村莊與小徑 看到 scoreborad 有人卡在最後一個 subtask，有點好奇究竟是單純的 bug 還是堅信 SPFA 的時間複雜度是 $O(kE)$ 而狂傳。大概在 $10$ 年前，筆者還在打 TOI 的時候，簡體中文網路上就流傳著 SPFA 時間複雜度只有 $O(2E)$，快到可以作為 general 最短路徑演算法的都市傳說。筆者並不清楚為什麼許多中國人認為 Dijkstra 比 SPFA 難寫（筆者覺得正好相反）導致即使可能 TLE 也要寫 SPFA，不過總之請記得，如果一個題目能用 DAG 上 DP 或 Dijkstra 過，請不要用 SPFA。 C. 樣本解析 這題的交集關係部分寫得很繁瑣，但我們沒有辦法。本來打算用 $\subset$ 表示 proper subset，實際上也有 $\subseteq$ 這個符號，筆者認為就像 $<$ 和 $\leq$ 一樣，不應有混淆的空間；然而偏偏有些作者在用「$A \subset B$」時，允許 $A = B$，可能導致參賽者混淆而放棄。也考慮過改用 $\subsetneq$ 符號，但這跟 $\lneq$ 一樣相對罕見，考慮參賽者都是高中生很可能看不懂，只好全部改用中文敘述。 D. 水果包裝 筆者第一次看到題目後，在紙上推敲了許久（$30$ 分鐘有）才得出 greedy 結論，很意外這題的答題狀況這麼好 ，好奇到底有多少人是用猜的 。不過有一等獎參賽者沒能拿到滿分，用心出 $n$ 的數量級 $10^5$ 的測資也有了價值 (? 原先這題 $n$ 的上限只到 $100$，給的 speci
張貼留言
閱讀完整內容

109 學年度全國資訊學科能力競賽各題詳解

筆者參與了這屆全國賽的驗題，也出了 pD 與 pG 的所有測試資料。由於現場講解有些不夠明確 ，故在這邊放一份兩位驗題者與筆者提供的詳解。題本的連結在 這裡 ，pE / pF / pG / pH 的時間限制分別為 2.0s / 2.3s / 6.5s / 0.1s，其餘題目皆為 1.0s。 A. 礦砂採集 這題是很典型的 連續背包問題 。結論非常簡單：只要不斷貪婪地將單位重量價值最大的礦砂放進背包，直到背包已滿或所有礦砂均已被放入，就能最大化總價值。 一個簡單的做法是將所有礦砂依照單位重量價值由大到小排序，依序放入背包直到滿即可。複雜度是 $O(n \log n)$。 線性做法 雖然並不是本題的考點，但有一個值得一提的 $O(n)$ 做法存在。以下為了方便說明，假定所有的 $x_i$ 均相異。 隨機選擇一個礦砂 $i$，並將所有的礦砂分為單位價值 $\ge x_i$ 與 $< x_i$ 兩堆。 分歧判斷： 若單位價值 $\ge x_i$ 的礦砂可以塞滿背包，則將 $< x_i$ 的礦砂全刪除，並往大的 $x$ 找答案。 反之則將價值 $\ge x_i$ 的礦砂全刪除，往小的 $x$ 找答案。 搜尋完後得到的值代表「總價值最大時，背包中單位重量價值最小的礦砂」，再用這個價值去反求答案。 演算法與 quickselect 非常相似，期望時間複雜度為 $O(n)$。 B. 村莊與小徑 這題是一道最短路徑的問題，但給定的限制中有幾個點要注意： 給定的圖是 DAG（有向無環圖）。 邊權可能是負的。 條件 1 保證這張圖存在拓樸排序，求解可用 top-down DP，或找出拓樸排序後用 bottom-up DP。 // ord = 拓樸排序的點順序 // fr[x] = 連到 x 的所有點 fill(dis, dis+n+ 1 , INF); dis[ 1 ] = 0 ; for ( int i= 1 ; i<=n; i++) { int p = ord[i]; // 找所有能連到 p 的點 j，更新 p 的最短距離 for (Edge j: fr[p]) dis[p] = m
張貼留言
閱讀完整內容

模 p 下的平方根: Cipolla 演算法

設 $p$ 為質數且 $a \in \mathbb{Z}$。考慮問題： 是否存在 $r \in \mathbb{Z}$ 使得 $r^2 \equiv a\ (\operatorname{mod}p)$？ 如果這樣的 $r$ 存在，有沒有好的方法找？ 如果第一個問題的答案是肯定的且 $p\nmid a$，我們說 $a$ 是 $p$ 的 二次剩餘 (quadratic residue)；如果第一個問題的答案是否定的，則說 $a$ 是 $p$ 的 二次非剩餘 (quadratic nonresidue)。 當 $p = 2$ 或 $a \equiv 0$ 時上面兩個問題都是 trivial；以下假定 $p \geq 3$ 且 $a \not\equiv 0$。透過觀察 $x^2-r^2 = (x-r)(x+r)$ 且 $r \neq -r$，我們發現 $a$ 可以寫成 $r^2$ 若且唯若方程式 $x^2-a = 0$ 在 $\mathbb{Z}_p$ 下恰有兩相異根。這代表恰有 $\frac{p-1}{2}$ 個 $\mathbb{Z}_p^\times$ ($\mathbb{Z}_p$ 的乘法群) 裡的元素能被開根號，而另外 $\frac{p-1}{2}$ 個 $\mathbb{Z}_p^\times$ 裡的元素不能被開根號。又，費馬小定理指出，對於所有的 $x \in \mathbb{Z}_p^\times$，均有 \[ x^{p-1} -1 = (x^\frac{p-1}{2}-1)(x^\frac{p-1}{2}+1) = 0 \] 若 $a = r^2$，則 $a^\frac{p-1}{2}-1 = r^{p-1}-1 = 0$。因為方程式 $x^\frac{p-1}{2}-1 = 0$ 最多只能有 $\frac{p-1}{2}$ 個根，我們得到了以下的定理： [定理] 設 $p \geq 3$ 為一奇質數且 $a \in \mathbb{Z}_p^\times$，則 $a$ 是 $p$ 的二次剩餘若且唯若 $a^\frac{p-1}{2} = 1$。 $a$ 是 $p$ 的二次非剩餘若且唯若 $a^\frac{p-1}{2} = -1$。 至此第一個問題 $O(\log p)$ 時間複雜度圓滿解決。 為了接下來的討論方便，這邊介紹 勒讓德符號 (Le
張貼留言
閱讀完整內容

(Debug) TIOJ 1752 妹妹的汽水

Description 雖然經歷了這場讓人魂飛魄散的事件，但是經過護士姊姊細心診斷確定他的人及屬性都沒受創之後，妁艷回到了家。 隔天去了學校，學習了更多技能之後發現身體感覺並沒有什麼異狀。可是體內感覺卻有股蠢蠢欲動的力量……。 回到了家，突然想到昨天妹妹借的書還沒還給他，就去找妹妹。可是，妁艷在門外叫了好幾聲都沒反應，他就逕自進入妹妹的房間。 「喔哈哈！」進來之後發現妹妹不在，妁艷不自覺的笑了。他開始尋找目標物，從書櫃、抽屜、書包、床鋪、衣櫃等等地方仔細搜索之後，終於在書桌上找到了那本書。 「奇怪？」書上放著一張紙條，使妁艷有點疑惑，上面寫著：「$2, 3, 5, 7, 11, 13, 17, \ldots$。」 聰明的妁艷當然一看又知道是一串質數。找的口有點渴的妁艷，拿起桌上喝了一半的汽水準備一飲而盡，猛然發現蓋子竟然打不開，而且瓶蓋上還印了一個正整數 $n$ 和一個質數 $p$，仔細一看他才發現紙上還寫了：「打開汽水需要找出第 $p$ 個冒出的泡泡編號。」 為了喝到汽水，妁艷研究出了這種汽水冒泡的規律。 泡泡原本的順序是 $n$ 到 $1$，也就是 $n, n-1, n-2, \ldots, 3, 2, 1$。 從時間 $t=0$ 開始每秒會有些泡泡跟其他泡泡位置交換。 奇妙的是，它們都遵守第 $t$ 秒內時只有被編號第 $t$ 個質數 $q$ 整除的泡泡才可能變位置。 第 $t$ 秒內，對第 $i$ 個被 $q$ 整除的泡泡編號 $a$ 會跟第 $i+1$ 個被 $q$ 整除的泡泡編號 $b$ 比大小，如果 $a$ 大於 $b$，泡泡 $a$ 和 $b$ 就會交換位置，$a$ 繼續跟第 $i+2$ 個比，否則用 $b$ 跟第 $i+2$ 個比。 泡泡最後的位置順序的倒序就是冒泡順序。 例如 $n=8$， $t=0$ 時，順序是 $8, 7, 6, 5, 4, 3, 2, 1$。 $t=1$ 時，順序是 $6, 7, 4, 5, 2, 3, 8, 1$。($8$ 跟 $6$ 換、$8$ 跟 $4$ 換、$8$ 跟 $2$ 換且 $2, 4, 6, 8$ 都被 $2$ 整除) $t=2$ 時，順序是 $3, 7, 4, 5, 2, 6, 8, 1$。($6$ 跟 $3$ 換且 $3, 6$ 都被 $3$ 整除)
張貼留言
閱讀完整內容

NTUJ 1697 Ancestors

圖片
Description You will be given a connected undirected tree. Each node will have an associated integer that we will call its value. We also define the value of a subset of nodes as the sum of values of the nodes in the subset. Consider the subsets of nodes of this tree whose size is between $1$ and $K$, inclusive, and satisfy the property that within each subset no node is an ancestor of another. We will call these subsets the $K$-anti-ancestral subsets of the tree. Your task is, given the tree, to find the $K$-anti-ancestral subset of maximum value. As an example, consider the tree below. Each node is named with a capital letter and the value of each node is the integer below the letter: Suppose $K = 3$. Then the subset of nodes $\{A\}, \{B, E\}, \{C, E\}, \{D, G\}$ and $\{B, E, F\}$ are some of the $K$-anti-ancestral subsets of the tree, because they all have between $1$ and $K = 3$ nodes and within each subset there doesn't exist a pair of nodes such that one is
張貼留言
閱讀完整內容