NTUJ 1697 Ancestors

Description

You will be given a connected undirected tree. Each node will have an associated integer that we will call its value. We also define the value of a subset of nodes as the sum of values of the nodes in the subset. Consider the subsets of nodes of this tree whose size is between $1$ and $K$, inclusive, and satisfy the property that within each subset no node is an ancestor of another. We will call these subsets the $K$-anti-ancestral subsets of the tree.

Your task is, given the tree, to find the $K$-anti-ancestral subset of maximum value.

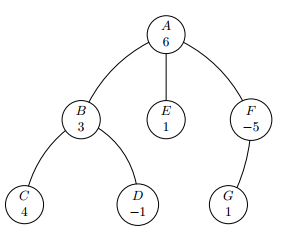
As an example, consider the tree below. Each node is named with a capital letter and the value of each node is the integer below the letter:

Suppose $K = 3$. Then the subset of nodes $\{A\}, \{B, E\}, \{C, E\}, \{D, G\}$ and $\{B, E, F\}$ are some of the $K$-anti-ancestral subsets of the tree, because they all have between $1$ and $K = 3$ nodes and within each subset there doesn't exist a pair of nodes such that one is an ancestor of the other.

On the other hand, $\{A, B\}$ is not a $K$-anti-ancestral subset because $A$ is an ancestor of $B$, $\{A, G\}$ isn't one because $A$ is an ancestor of $G$ and $\{C, B, D\}$ isn't one either because $B$ is an ancestor of both $C$ and $D$. The subset $\{C, D, E, F\}$, even though it doesn't contain a node that is an ancestor of another one, is not a $K$-anti-ancestral subset because it has $4 > K = 3$ nodes. Similarly, the empty set $\emptyset$ is not one either because it contains $0$ elements.

The value of the $K$-anti-ancestral subset $\{A\}$ is $6$; the value of $\{B, E\}$ is $3 + 1 = 4$; the value of $\{C, E\}$ is $4 + 1 = 5$; the value of $\{D, G\}$ is $-1 + 1 = 0$ and the value of $\{B, E, F\}$ is $3 + 1 + (-5) = -2$. Since the tree is small, it's easy to convince yourself by inspection that the maximum possible value of any $K$-anti-ancestral subset is $6$. However, notice that there might be several ways to achieve the maximum value: $\{A\}$ and $\{C, E, G\}$ both have value $6$. You are only asked to find the value of the maximum $K$-anti-ancestral subset so it doesn't really matter how many of them exist.

Input

The input contains several test cases (at most $50$). Each test case is described on three lines:

The first line contains two integers $n$ and $K$, the number of nodes in the tree and the parameter $K$ as explained above. Assume $2 \leq n \leq 10^5$ and $1 \leq K \leq 100$ (notice that these constraints guarantee that there will always exist at least one $K$-anti-ancestral subset, e.g. by taking a single node). The nodes will be numbered $0$ through $n-1$. The root of the tree will always be node $0$. You can assume that the tree will always be connected, i.e., there will always exist a path connecting any pair of nodes.

The second line contains $n$ integers separated by spaces. These integers represent the values of nodes $0$ through $n-1$ (the first integer is the value of node $0$, the second integer is the value of node $1$ and so on ~ the last integer is the value of node $n-1$). The value of any node will always be between $-100$ and $100$, inclusive.

The third line contains the description of the tree. It contains $n-1$ integers separated by spaces that represent the parent nodes of nodes $1$ through $n-1$ (the first integer is the parent of node $1$, the second integer is the parent of node $2$ and so on ~ the last integer is the parent of node $n-1$). Notice that since $0$ is always the root of the tree it doesn't have a parent and that's why this line contains only $n-1$ numbers instead of $n$.

The last line contains two zeros and should not be processed. See the sample input for clarification about this format. The first test case is the tree given in the figure above.

Output

For each test case, output the maximum possible value of any $K$-anti-ancestral subset on a single line.

Sample Input

7 3

6 3 4 -1 1 -5 1

0 1 1 0 0 5

2 1

-1 1

0

3 3

1 2 3

0 0

8 8

1 2 3 4 5 6 7 8

0 1 2 3 4 5 6

4 4

-27 -45 -67 -98

2 0 2

0 0

Sample Output

6

1

5

8

-27

Solution

這題可以看作加了一些限制的背包問題。不難想到下面這個 DP 解法：設 $D(u, w)$ 表示從 $T(u)$ (以 $u$ 為根的子樹) 拿恰好 $w$ 個節點，能達到的最大權重和。假定 $u$ 的子節點是 $v_1, v_2, \ldots, v_k$，只要進一步設 $D'(u, i, w)$ 為「從 $T(v_1), \ldots, T(v_i)$ 拿恰好 $w$ 個節點能達到的最大權重和」，就得到

\begin{equation}\label{dp1}D'(u, i, w) = \max_{0 \leq j \leq w}\{D'(u, i-1, j)+D(v_i, w-j)\}.\end{equation}

但不幸的是這個 DP 的時間複雜度是 $O(nK^2)$。可是一般的背包 DP 時間複雜度是 $O(nK)$ 啊！問題出在哪裡？

讓我們回想一下一般背包 DP 的轉移式： \begin{equation}\label{dp2}D(i, w) = \max\{D(i-1, w), D(i-1, w-c_i)+p_i\},\end{equation} 其中 $D(i, w)$ 表示「從物品 $1, \ldots, i$ 中，拿到總重恰為 $w$，能達到的最大價值」，$c_i$ 為物品 $i$ 的重量，$p_i$ 為物品 $i$ 的價值。可以發現，$(\ref{dp1})$ 的轉移，必須考慮「該從 $T(v_i)$ 拿出多少節點」，但 $(\ref{dp2})$ 只需要考慮「要不要拿物品 $i$」。

由於 $(\ref{dp1})$ 的計算看起來逃脫不了 $O(K)$，狀態必須重新設計。考慮這棵樹的一個走訪 (traversal) $u_1, \ldots, u_n$，模仿 $(\ref{dp2})$，定義 $D(i, w)$ 為「從 $u_1, \ldots, u_i$ 中，拿恰好 $w$ 個頂點，能達到的最大價值」。這樣一來就得到 \[D(i, w) = \max\{D(i-1, w), D(\operatorname{loli}(i), w-1)+p_i\},\] 其中 $p_i$ 為 $u_i$ 的權重。等等！$\operatorname{loli}(i)$ 是什麼？由於拿了 $u_i$，就不能拿 $u_i$ 的任何子孫，我們希望對於每個 $i$，均有 \[``1 \leq j < i\text{ and }u_j \notin T(u_i)" \ \Longleftrightarrow\ 1 \leq j \leq \operatorname{loli}(i).\]

顯然並不是每種走訪方式都找得到 $\operatorname{loli}$ 函數。一種找得到 $\operatorname{loli}$ 的走訪方式是從 $0$ 開始 DFS，令 $u_i$ 為第 $i$ 個離開的節點，我們就有 $\operatorname{loli}(i) = i - |T(u_i)|$，整個問題 $O(nK)$ 圓滿解決。

其實這已經不算樹上 DP 了，因為得到了 $u_1, \ldots, u_n$ 和 $\operatorname{loli}$ 後，DP 的計算方式完全脫離了樹的依賴關係。

我的 code：

https://ideone.com/R3eeRb