NTUJ 1697 Ancestors
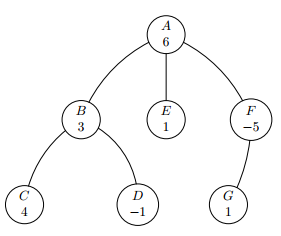
Description You will be given a connected undirected tree. Each node will have an associated integer that we will call its value. We also define the value of a subset of nodes as the sum of values of the nodes in the subset. Consider the subsets of nodes of this tree whose size is between $1$ and $K$, inclusive, and satisfy the property that within each subset no node is an ancestor of another. We will call these subsets the $K$-anti-ancestral subsets of the tree. Your task is, given the tree, to find the $K$-anti-ancestral subset of maximum value. As an example, consider the tree below. Each node is named with a capital letter and the value of each node is the integer below the letter: Suppose $K = 3$. Then the subset of nodes $\{A\}, \{B, E\}, \{C, E\}, \{D, G\}$ and $\{B, E, F\}$ are some of the $K$-anti-ancestral subsets of the tree, because they all have between $1$ and $K = 3$ nodes and within each subset there doesn't exist a pair of nodes such that one is ...